题目内容
求下列函数的定义域:(1)y=![]() ;(2)y=
;(2)y=![]() .
.
解:(1)要使函数有意义,必须且只需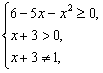 即
即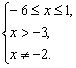
∴-3<x<-2或-2<x≤1.
因此函数的定义域为(-3,-2)∪(-2,1].
(2)要使函数有意义,必须且只需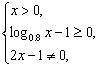 即
即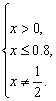
∴0<x≤![]() 且x≠
且x≠![]() .
.
因此函数的定义域是(0,![]() )∪(
)∪(![]() ,
,![]() ].
].
点评:求函数的定义域是研究函数性质的基础,求含对数符号的函数的定义域就要使对数符号后面的真数大于零,如果底数中也含有自变量就要使底数大于零且不等于1.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目