题目内容
设f(x)=asin(π-2x)+bsin(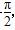 +2x),其中a,b∈R,ab≠0,若f(x)≤|f(
+2x),其中a,b∈R,ab≠0,若f(x)≤|f(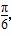 )|对一切x∈R恒成立,则
)|对一切x∈R恒成立,则
①f( )=0
)=0
②f(x)的周期为2π
③f(x)既不是奇函数也不是偶函数
④存在经过点(a,b)的直线与函数f(x)的图象不相交
以上结论正确的是________.(写出所有正确结论的编号)
①③
[解析] f(x)=asin(π-2x)+bsin(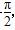 +2x)=asin2x+bcos2x=
+2x)=asin2x+bcos2x= sin(2x+φ),其中,tanφ=
sin(2x+φ),其中,tanφ= ,
,
∵f(x)≤|f( )|对一切x∈R恒成立,
)|对一切x∈R恒成立,
∴|f(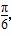 )|=
)|= ,∴2×
,∴2× +φ=kπ+
+φ=kπ+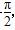 ,
,
∴φ=kπ+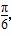 ,
,
又f(x)的周期T=π,故①③正确,②④错误.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,α∈(0,π),则tanα=( )
,α∈(0,π),则tanα=( )
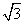 sin2x+m-1=0在x∈(
sin2x+m-1=0在x∈( ,π)上有两个不同的实数根,则m的取值范围是________.
,π)上有两个不同的实数根,则m的取值范围是________. ,sin(α-β)=-
,sin(α-β)=- ,α、β均为锐角,则β等于( )
,α、β均为锐角,则β等于( )
 sinxcosx-cos2x-
sinxcosx-cos2x- ,x∈R.
,x∈R.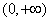 上为增函数的是( )
上为增函数的是( )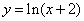 B.
B.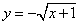 C.
C.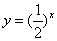 D.
D.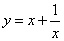
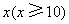 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为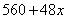 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用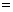 平均建筑费用
平均建筑费用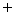 平均购地费用,平均购地费用
平均购地费用,平均购地费用 )
)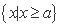 ,若A∪B=B,则实数a的取值范围是 .
,若A∪B=B,则实数a的取值范围是 .