题目内容
已知函数f(x)＝
sinxcosx－cos2x－
，x∈R.
(1)求函数f(x)的最小值和最小正周期；
(2)已知△ABC内角A、B、C的对边分别为a、b、c，且c＝3，f(C)＝0，若向量m＝(1，sinA)与n＝(2，sinB)共线，求a、b的值．
(1)f(x)＝sinxcosx－cos2x－＝
sin2x－cos2x－1＝sin(2x－
)－1，
∴f(x)的最小值是－2，最小正周期为π.
(2)∵f(C)＝sin(2C－)－1＝0，即sin(2C－)＝1，
∵0<C<π，－<2C－<
，
∴2C－＝
，∴C＝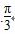
.
∵m与n共线，∴sinB－2sinA＝0.
由正弦定理
＝
，得b＝2a，①
∵c＝3，由余弦定理得，9＝a2＋b2－2abcos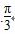，②
解方程组①②得，
练习册系列答案
相关题目
是第几象限的角？
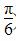)＝2，且f(x)的导函数f ′(x)的图象关于直线x＝
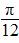对称．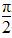
]上总有实数解，求实数k的取值范围．
有意义，则m的取值范围是________．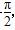
＋2x)，其中a，b∈R，ab≠0，若f(x)≤|f(
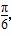)|对一切x∈R恒成立，则
)＝0
B.
D．1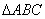
的两边AB、AC互相垂直，则
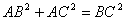。”拓展到空间，类比平面几何的勾股定理，研究三棱锥的侧面积与底面积间的关系，可以得到的正确结论是：“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直，则 ”。