题目内容
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,
函数f(x)=Asin(ωx+φ)(A>0,ω>0,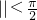 )的一段图象如图所示.
)的一段图象如图所示.
(1)求函数y=f(x)的解析式;
(2)将函数y=f(x)的图象向右平移 个单位,得到y=g(x)的图象,求函数h(x)=f(x)+g(x)的图象的对称轴和对称中心.
个单位,得到y=g(x)的图象,求函数h(x)=f(x)+g(x)的图象的对称轴和对称中心.
解:(1)由图知A=2,T=π,于是 ,
,
将y=2sin2x的图象向左平移 个单位长度,得y=2sin(2x+Φ)的图象.
个单位长度,得y=2sin(2x+Φ)的图象.
于是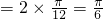 ,∴
,∴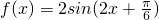 .…(6分)
.…(6分)
(2)依题意得 .…(8分)
.…(8分)
故h(x)=f(x)+g(x)=
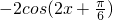 =
= .…(10分)
.…(10分)
由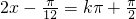 ,得
,得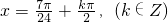 .
.
由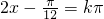 ,得
,得 .
.
∴h(x)的对称轴为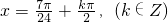 ,对称中心为
,对称中心为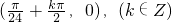 …(13分)
…(13分)
分析:(1)由图知A=2,T=π,于是 ,题中的图象可看作是y=2sin2x的图象向左平移
,题中的图象可看作是y=2sin2x的图象向左平移 个单位长度,可求Φ值;
个单位长度,可求Φ值;
(2)由(1)的方法可求g(x)的解析式,从而可求h(x)的解析式,利用整体法的思想易求得h(x)的对称轴和对称中心.
点评:本题为三角函数的图象与性质的综合应用,处理好图象的变换是解决问题的关键,属中档题.
 ,
,将y=2sin2x的图象向左平移
 个单位长度,得y=2sin(2x+Φ)的图象.
个单位长度,得y=2sin(2x+Φ)的图象.于是
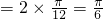 ,∴
,∴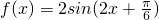 .…(6分)
.…(6分)(2)依题意得
 .…(8分)
.…(8分)故h(x)=f(x)+g(x)=

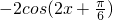 =
= .…(10分)
.…(10分)由
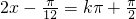 ,得
,得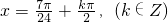 .
.由
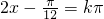 ,得
,得 .
.∴h(x)的对称轴为
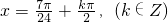 ,对称中心为
,对称中心为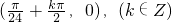 …(13分)
…(13分)分析:(1)由图知A=2,T=π,于是
 ,题中的图象可看作是y=2sin2x的图象向左平移
,题中的图象可看作是y=2sin2x的图象向左平移 个单位长度,可求Φ值;
个单位长度,可求Φ值;(2)由(1)的方法可求g(x)的解析式,从而可求h(x)的解析式,利用整体法的思想易求得h(x)的对称轴和对称中心.
点评:本题为三角函数的图象与性质的综合应用,处理好图象的变换是解决问题的关键,属中档题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 如图,是函数f(x)=Asin(φx+φ)(其中A>0,φ>0,0<φ<π)的部分图象,则其解析为
如图,是函数f(x)=Asin(φx+φ)(其中A>0,φ>0,0<φ<π)的部分图象,则其解析为 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<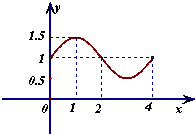 函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(0)+f(1)+f(2)+…+f(2008)的值分别为( )
函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(0)+f(1)+f(2)+…+f(2008)的值分别为( )