题目内容
已知函数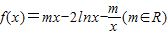
(1)若f'(1)=2,求m的值;
(2)若函数y=f(x)在[1,+∞)上为单调函数,求m的取值范围.
【答案】分析:(1)求出原函数的导函数直接由f'(1)=2列式求m的值;
(2)求出原函数的导函数,由函数y=f(x)在[1,+∞)上为单调函数,得其导函数[1,+∞)上大于等于0或小于等于0恒成立,然后利用基本不等式求解m的取值范围.
解答:解:(1) ,由已知,f'(1)=m-2+m=2,
,由已知,f'(1)=m-2+m=2,
所以m=2;
(2)若函数y=f(x)在[1,+∞)上为单调函数,则在[1,+∞)上
有 恒成立,或
恒成立,或 恒成立
恒成立
即 ,或
,或 对x∈[1,+∞)恒成立,
对x∈[1,+∞)恒成立,
因为 ,
,
而当x∈[1,+∞)时, ∈[2,+∞),故
∈[2,+∞),故 ,
,
所以m≥1或m≤0.
即m的取值范围是m≥1或m≤0.
点评:本题考查了函数的单调性和导数的关系,训练了利用基本不等式求函数的最值,考查了分离变量法,是中档题.
(2)求出原函数的导函数,由函数y=f(x)在[1,+∞)上为单调函数,得其导函数[1,+∞)上大于等于0或小于等于0恒成立,然后利用基本不等式求解m的取值范围.
解答:解:(1)
 ,由已知,f'(1)=m-2+m=2,
,由已知,f'(1)=m-2+m=2,所以m=2;
(2)若函数y=f(x)在[1,+∞)上为单调函数,则在[1,+∞)上
有
 恒成立,或
恒成立,或 恒成立
恒成立即
 ,或
,或 对x∈[1,+∞)恒成立,
对x∈[1,+∞)恒成立,因为
 ,
,而当x∈[1,+∞)时,
 ∈[2,+∞),故
∈[2,+∞),故 ,
,所以m≥1或m≤0.
即m的取值范围是m≥1或m≤0.
点评:本题考查了函数的单调性和导数的关系,训练了利用基本不等式求函数的最值,考查了分离变量法,是中档题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
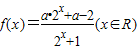

 时,|f(x)|≤4恒成立,求实数m的取值范围.
时,|f(x)|≤4恒成立,求实数m的取值范围.