题目内容
已知函数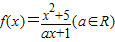
(1)若f(x)在[1,3]上单调递增,求a的取值范围;
(2)若f(x)在x=x1,x=x2处取极值,且满足|f(x1)-f(x2)|≤|x1-x2|,求a的取值范围.
【答案】分析:(1)若f(x)在[1,3]上单调递增,则函数的导数在[1,3]上大于0恒成立,得到关于x的二次函数,只要二次函数图象当x∈[1,3]时恒在x轴上方即可,再利用二次函数根的分布来判断即可.
(2)若f(x)在x=x1,x=x2处取极值,则x1,x2是方程g(x)=ax2+2x-5a=0的两根,利用韦达定理可得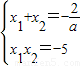 ,把|f(x1)-f(x2)|≤|x1-x2|中的f(x1)和f(x2)用x1,x2表示,化简,即可求出a的范围.
,把|f(x1)-f(x2)|≤|x1-x2|中的f(x1)和f(x2)用x1,x2表示,化简,即可求出a的范围.
解答:解:(1)∵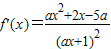 ,
,
∴由f(x)在[1,3]上单调递增得: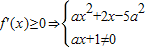 .
.
令g(x)=ax2+2x-5a,则得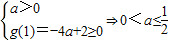 ;
;
或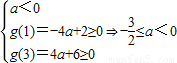 ;
;
又当a=0时,g(x)=2x>0在[1,3]上恒成立,∴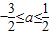
再由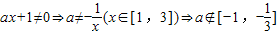 .
.
综上,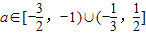
(2)∵f(x)在x=x1,x=x2处取极值,∴x1,x2是方程g(x)=ax2+2x-5a=0的两根,
∴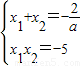 ,
,
∴由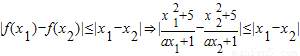
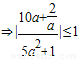 ,
,
∴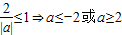 .
.
点评:本题主要考查了应用导数求函数的单调区间,极值,属于导数的应用.
(2)若f(x)在x=x1,x=x2处取极值,则x1,x2是方程g(x)=ax2+2x-5a=0的两根,利用韦达定理可得
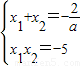 ,把|f(x1)-f(x2)|≤|x1-x2|中的f(x1)和f(x2)用x1,x2表示,化简,即可求出a的范围.
,把|f(x1)-f(x2)|≤|x1-x2|中的f(x1)和f(x2)用x1,x2表示,化简,即可求出a的范围.解答:解:(1)∵
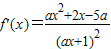 ,
,∴由f(x)在[1,3]上单调递增得:
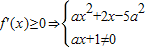 .
.令g(x)=ax2+2x-5a,则得
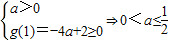 ;
;或
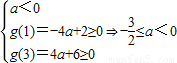 ;
;又当a=0时,g(x)=2x>0在[1,3]上恒成立,∴
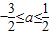
再由
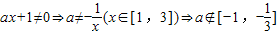 .
.综上,
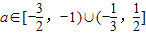
(2)∵f(x)在x=x1,x=x2处取极值,∴x1,x2是方程g(x)=ax2+2x-5a=0的两根,
∴
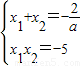 ,
,∴由
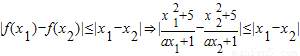
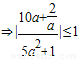 ,
,∴
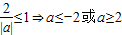 .
.点评:本题主要考查了应用导数求函数的单调区间,极值,属于导数的应用.

练习册系列答案
相关题目
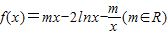
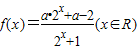

 时,|f(x)|≤4恒成立,求实数m的取值范围.
时,|f(x)|≤4恒成立,求实数m的取值范围.