题目内容
(本小题满分13分)在某校组织的一次篮球定点投篮训练中,规定每人最多投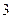 次;在
次;在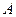 处每投进一球得
处每投进一球得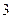 分,在
分,在 处每投进一球得
处每投进一球得 分;如果前两次得分之和超过
分;如果前两次得分之和超过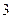 分即停止投篮,否则投第三次,某同学在
分即停止投篮,否则投第三次,某同学在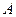 处的命中率
处的命中率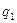 为
为 ,在
,在 处的命中率为
处的命中率为 ,该同学选择先在
,该同学选择先在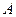 处投一球,以后都在
处投一球,以后都在 处投,用
处投,用 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
(1)求 的值;
的值;
(2)求随机变量 的数学期望E
的数学期望E .
.
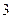 次;在
次;在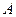 处每投进一球得
处每投进一球得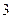 分,在
分,在 处每投进一球得
处每投进一球得 分;如果前两次得分之和超过
分;如果前两次得分之和超过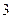 分即停止投篮,否则投第三次,某同学在
分即停止投篮,否则投第三次,某同学在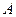 处的命中率
处的命中率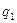 为
为 ,在
,在 处的命中率为
处的命中率为 ,该同学选择先在
,该同学选择先在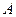 处投一球,以后都在
处投一球,以后都在 处投,用
处投,用 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为  | 0 | 2 | 3 | 4 | 5 |
| p | 0.03 | P1 | P2 | P3  | P4 |
 的值;
的值; (2)求随机变量
 的数学期望E
的数学期望E .
.(1)q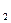 =0.8;
=0.8;
(2)
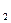 =0.8;
=0.8; (2)

(1)设该同学在A处投中为事件A,在B处投中为事件B,则事件A,B相互独立,且P(A)=0.25,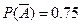 , P(B)= q
, P(B)= q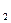 ,
, .
.
根据分布列知: =0时
=0时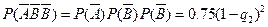 =0.03,
=0.03,
所以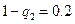 ,q
,q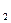 =0.8.………………………………
=0.8.……………………………… ….3分
….3分
(2)当 =2时, P1=
=2时, P1=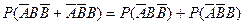 ……………………….5分
……………………….5分
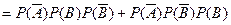 =0.75
=0.75
q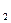 (
(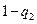 )×2=1.5 q
)×2=1.5 q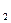 (
(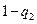 )=0.24
)=0.24
当 =3
=3 时, P2 =
时, P2 =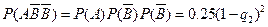 =0.01, ………….7分
=0.01, ………….7分
当 =4时, P3=
=4时, P3=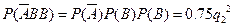 =0.48, …………………….9分
=0.48, …………………….9分
当 =5时, P4=
=5时, P4=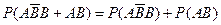
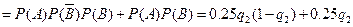 =0.24……………………11分
=0.24……………………11分
所以随机变量 的分布列为
的分布列为
随机变量 的数学期望
的数学期望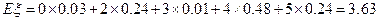
……………………….13分
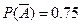 , P(B)= q
, P(B)= q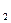 ,
, .
.根据分布列知:
 =0时
=0时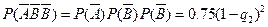 =0.03,
=0.03,所以
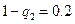 ,q
,q =0.8.………………………………
=0.8.……………………………… ….3分
….3分(2)当
 =2时, P1=
=2时, P1=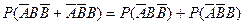 ……………………….5分
……………………….5分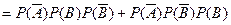 =0.75
=0.75 q
 (
(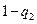 )×2=1.5 q
)×2=1.5 q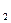 (
(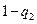 )=0.24
)=0.24当
 =3
=3 时, P2 =
时, P2 =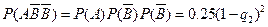 =0.01, ………….7分
=0.01, ………….7分当
 =4时, P3=
=4时, P3=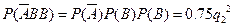 =0.48, …………………….9分
=0.48, …………………….9分当
 =5时, P4=
=5时, P4=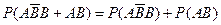
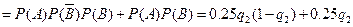 =0.24……………………11分
=0.24……………………11分所以随机变量
 的分布列为
的分布列为  | 0 | 2 | 3 | 4 | 5 |
| p | 0.03 | 0.24 | 0.01 | 0.48 | 0.24 |
 的数学期望
的数学期望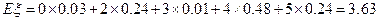
……………………….13分

练习册系列答案
相关题目
 ,从中任取三个数,则至少有两个数位于同行或同列的概率是 ( )
,从中任取三个数,则至少有两个数位于同行或同列的概率是 ( )








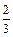 ,每次考科目B成绩合格的概率均为
,每次考科目B成绩合格的概率均为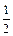 。假设他在这项考试中不放弃所有的考试机会,且每次的考试成绩互不影响,记他参加考试的次数为
。假设他在这项考试中不放弃所有的考试机会,且每次的考试成绩互不影响,记他参加考试的次数为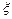 .
.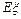 ;
; 书的概率.
书的概率. 若小张参加每次考核合格的概率依次组成一个公差为
若小张参加每次考核合格的概率依次组成一个公差为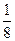 的等差数列,他参加第一次考核合格的概率超过
的等差数列,他参加第一次考核合格的概率超过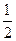 ,且他直到参加第二次考核才合格的概率为
,且他直到参加第二次考核才合格的概率为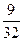
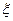 和分布列和数学期望值
和分布列和数学期望值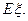
 与产量
与产量 的函数关系式为
的函数关系式为
 与产量
与产量


 分别表示市场情形好、中差时的利润,随机变量
分别表示市场情形好、中差时的利润,随机变量 ,表示当产量为
,表示当产量为 ;
; 如下:若是白色,则
如下:若是白色,则 ;若是黄色,则
;若是黄色,则 ;若是红色,则
;若是红色,则 ;若卡片数字是
;若卡片数字是 ,则
,则

 与数字方差
与数字方差
 ,且各次射击的结果互不影响。
,且各次射击的结果互不影响。 为射手射击3次后的总的分数,求
为射手射击3次后的总的分数,求 元,求
元,求 的观测值过程如下:
的观测值过程如下: ;类比甲的算法试计算语文
;类比甲的算法试计算语文