题目内容
设数列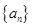 的前
的前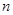 项和为
项和为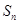 ,且方程
,且方程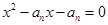 有一个根为
有一个根为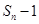 ,
,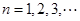 .
.
(1)证明:数列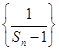 是等差数列;
是等差数列;
(2)设方程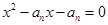 的另一个根为
的另一个根为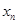 ,数列
,数列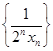 的前
的前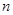 项和为
项和为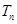 ,求
,求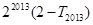 的值;
的值;
(3)是否存在不同的正整数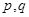 ,使得
,使得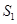 ,
,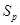 ,
,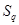 成等比数列,若存在,求出满足条件的
成等比数列,若存在,求出满足条件的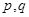 ,若不存在,请说明理由.
,若不存在,请说明理由.
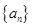 的前
的前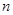 项和为
项和为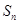 ,且方程
,且方程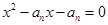 有一个根为
有一个根为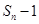 ,
,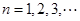 .
.(1)证明:数列
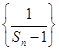 是等差数列;
是等差数列;(2)设方程
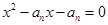 的另一个根为
的另一个根为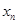 ,数列
,数列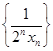 的前
的前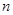 项和为
项和为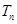 ,求
,求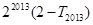 的值;
的值;(3)是否存在不同的正整数
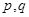 ,使得
,使得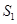 ,
,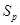 ,
,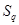 成等比数列,若存在,求出满足条件的
成等比数列,若存在,求出满足条件的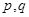 ,若不存在,请说明理由.
,若不存在,请说明理由.(1)利用等差数列的定义证明即可,(2)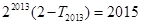 ,(3)存在不同的正整数
,(3)存在不同的正整数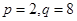 ,使得
,使得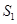 ,
,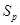 ,
,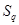 成等比数列
成等比数列
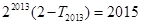 ,(3)存在不同的正整数
,(3)存在不同的正整数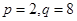 ,使得
,使得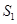 ,
,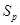 ,
,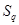 成等比数列
成等比数列试题分析:(1)∵
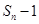 是方程
是方程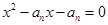 的根,
的根,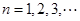
∴
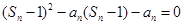
当
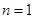 时,
时,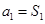 ,∴
,∴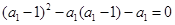 ,
,解得
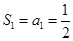 ,∴
,∴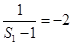 2分
2分当
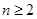 时,
时,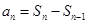 ,∴
,∴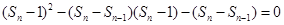
化简得
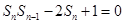 ,∴
,∴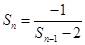 ,∴
,∴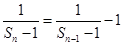 ,
,∴
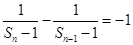 ,又
,又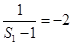 5分
5分∴数列
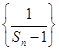 是以
是以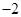 为首项,
为首项,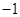 为公差的等差数列 6分
为公差的等差数列 6分(2)由(1)得,
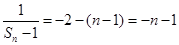
∴
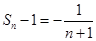 ,带入方程得,
,带入方程得,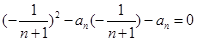 ,∴
,∴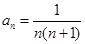 ,
,∴原方程为
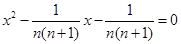 ,∴
,∴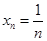 ,∴
,∴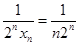 8分
8分∴
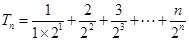 ①
①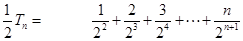 ②
②① — ②得
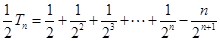
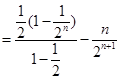
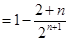 11分
11分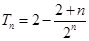 ,∴
,∴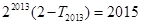 12分
12分(3)由(1)得,
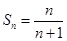 ,假设存在不同的正整数
,假设存在不同的正整数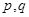 ,使得
,使得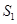 ,
,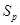 ,
,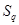 成等比数列,则
成等比数列,则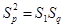
即
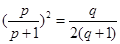 ,∵
,∵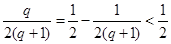 14分
14分∴
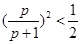 ,化简得,
,化简得,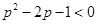
∴
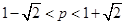 ,又∵
,又∵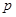
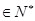 ,且
,且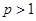
∴
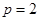 ∴
∴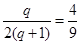 ,∴
,∴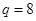 16分
16分∴存在不同的正整数
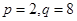 ,使得
,使得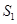 ,
,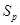 ,
,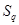 成等比数列
成等比数列点评:数列的通项公式及应用是数列的重点内容,数列的大题对逻辑推理能力有较高的要求,在数列中突出考查学生的理性思维,这是近几年新课标高考对数列考查的一个亮点,也是一种趋势.随着新课标实施的深入,高考关注的重点为等差、等比数列的通项公式,错位相减法、裂项相消法等求数列的前n项的和等等

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
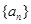 ,前
,前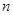 项和为
项和为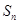 . 且满足
. 且满足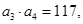
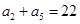 .
.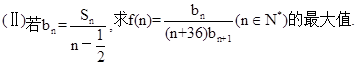
 的前n项和为
的前n项和为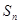 ,
,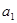 =1,且
=1,且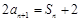
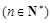 .
.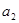 ,
,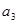 的值,并求数列
的值,并求数列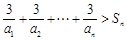
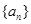 ,
,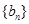 的前
的前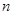 项和分别为
项和分别为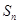 ,
,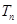 ,若
,若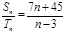 ,则使
,则使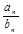 为整数的正整数n的取值个数是( )
为整数的正整数n的取值个数是( )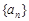 为等差数列,且
为等差数列,且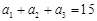
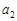 ;
;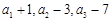 成等比数列,求数列
成等比数列,求数列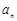 .
. 的前
的前 项和
项和 ,且满足
,且满足 .
. 的值,猜想
的值,猜想 是数列
是数列 的前
的前 .
.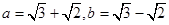 ,则
,则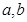 的等差中项为( )
的等差中项为( )



 中,已知
中,已知 ,
, ,
, ,则
,则 是( )
是( )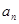 }是等差数列,
}是等差数列,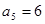 ,
,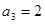 时,若自然数
时,若自然数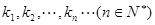 满足
满足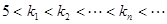 ,使得
,使得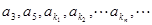 成等比数列,(1)求数列{
成等比数列,(1)求数列{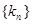 的通项公式及其前n项的和
的通项公式及其前n项的和