题目内容
【题目】在三棱锥
中，
，
在底面
上的投影为
的中点
，
.有下列结论：
①三棱锥的三条侧棱长均相等；
②
的取值范围是
；
③若三棱锥的四个顶点都在球
的表面上，则球的体积为
；
④若
，
是线段
上一动点，则
的最小值为
.
其中所有正确结论的编号是（ ）
A.①②B.②③C.①②④D.①③④
【答案】C
【解析】
根据三角形全等判断①，根据
的值和三角形的内角和得出
的范围，计算外接球半径判断③，将棱锥侧面展开计算最短距离判断④．
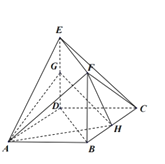
解：如图1，
，
是
的中点，
，
又
平面
，
，
，故①正确；
，
，又
，
，
过
作
，
为垂足，如图2，则
，
又
，
，
，故②正确；
，
为平面截三棱锥外接球的截面圆心，
设外接球球心为
，则在直线
上，如图3，
设
，则
，解得
，故为外接球的球心．
外接球的体积为
，故③错误．
若
，则
，又
，故
是等边三角形，
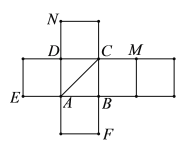
将平面
沿
翻折到平面
上，如图4，图5.
则
的最短距离为线段
的长．
，，
，
，故④正确．
故选：
．
练习册系列答案
天天练口算系列答案
相关题目
