题目内容
在直角坐标系中，已知两点M（4，2），N（1，-3），沿x轴把直角坐标平面折成直二面角后，M，N两点的距离为（ ）A．
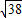
B．
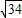
C．
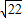
D．
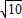
【答案】分析：设一、二象限所在的半平面为α，三、四象限所在的半平面为β，可得α⊥β．作MC⊥x轴于点C，连结NC、MN，可得MC⊥平面β，Rt△MNC中算出直角边CM、CN之长，再利用勾股定理算出MN长，即得M，N两点的距离．
解答：解：过点M作MC⊥x轴于点C，连结NC、MN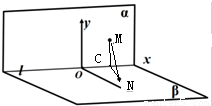
设一、二象限所在的半平面为α，三、四象限所在的半平面为β，
∵α-l-β是直二面角，α∩β=l，MC⊥l
∴MC⊥平面β
∵C的坐标（4，0），得MC=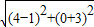
=3
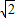
∴Rt△MNC中，MN=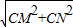
=
=
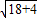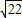
故选：C
点评：本题将直角坐标平面折叠，求折叠后的两点之间的距离．着重考查了面面垂直的性质定理、两点距离公式和勾股定理等知识，属于中档题．
解答：解：过点M作MC⊥x轴于点C，连结NC、MN
设一、二象限所在的半平面为α，三、四象限所在的半平面为β，
∵α-l-β是直二面角，α∩β=l，MC⊥l
∴MC⊥平面β
∵C的坐标（4，0），得MC=
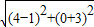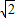
=3∴Rt△MNC中，MN=
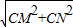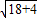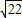
==故选：C
点评：本题将直角坐标平面折叠，求折叠后的两点之间的距离．着重考查了面面垂直的性质定理、两点距离公式和勾股定理等知识，属于中档题．
练习册系列答案
相关题目
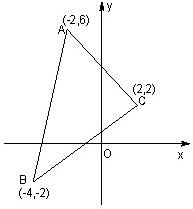如图，在直角坐标系中，已知△ABC的三个顶点的坐标，求：
如图，在直角坐标系中，已知射线OA：x-y=0（x≥0），OB：