题目内容
过双曲线E:
-
=1(b>a>0)的左顶点A作斜率为1的直线l,若l与双曲线E的两条渐近线相交于B,C两点,且|AB|=|BC|,则双曲线E的离心率为
.
| x2 |
| a2 |
| y2 |
| b2 |
| 10 |
| 10 |
分析:先根据条件求出直线l的方程,联立直线方程与渐近线方程分别求出点B,C的横坐标,结合B为AC的中点求出b,a间的关系,进而求出双曲线的离心率.
解答:解:由题得:双曲线:的左顶点A(a,0)
所以所作斜率为1的直线l:y=x+a,
若l与双曲线M的两条渐近线分别相交于点B(x1,y1),C(x2,y2).
联立其中一条渐近线y=-
x,则
,解得x1=
①;
同理联立
,解得x2=
②;
又因为|AB|=|BC|,
故B是A,C的中点,
∴x1=
⇒2x1=x2+a,
把①②代入整理得:b=3a,
∴e=
=
=
=
.
故答案为;
.
所以所作斜率为1的直线l:y=x+a,
若l与双曲线M的两条渐近线分别相交于点B(x1,y1),C(x2,y2).
联立其中一条渐近线y=-
| b |
| a |
|
| a2 |
| -a-b |
同理联立
|
| a2 |
| b-a |
又因为|AB|=|BC|,
故B是A,C的中点,
∴x1=
| x2+a |
| 2 |
把①②代入整理得:b=3a,
∴e=
| c |
| a |
| ||
| a |
| ||
| a |
| 10 |
故答案为;
| 10 |
点评:本题考题双曲线性质的综合运用,解题过程中要注意由|AB|=|BC|得到B是A,C的中点这以结论的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
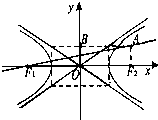 如图,已知双曲线E:
如图,已知双曲线E: