题目内容
已知数列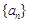 满足:
满足: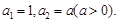 数列
数列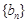 满足
满足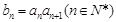 。
。
(1)若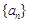 是等差数列,且
是等差数列,且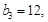 求
求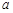 的值及
的值及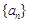 的通项公式;
的通项公式;
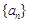 满足:
满足: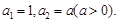 数列
数列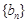 满足
满足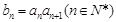 。
。(1)若
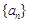 是等差数列,且
是等差数列,且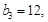 求
求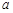 的值及
的值及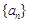 的通项公式;
的通项公式;(2)当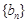 是公比为
是公比为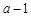 的等比数列时,
的等比数列时,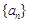 能否为等比数列?若能,求出
能否为等比数列?若能,求出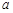 的值;若不能,请说明理由.(1)
的值;若不能,请说明理由.(1)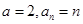 ;(2)数列
;(2)数列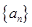 不能为等比数列.
不能为等比数列.
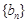 是公比为
是公比为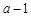 的等比数列时,
的等比数列时,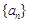 能否为等比数列?若能,求出
能否为等比数列?若能,求出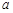 的值;若不能,请说明理由.(1)
的值;若不能,请说明理由.(1)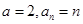 ;(2)数列
;(2)数列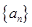 不能为等比数列.
不能为等比数列.试题分析:(1)由数列
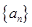 是等差数列,以及已知
是等差数列,以及已知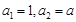 ,不难用
,不难用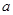 表示出
表示出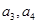 ,又由
,又由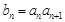 ,可得到
,可得到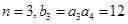 ,这样就可求出
,这样就可求出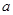 的值,根据等差数列的通项公式
的值,根据等差数列的通项公式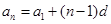 ,即可求得
,即可求得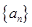 的通项公式; (2)由
的通项公式; (2)由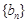 是等比数列且
是等比数列且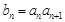 ,易得
,易得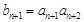 ,两式相比得
,两式相比得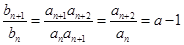 ,由此推出
,由此推出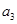 的值,又如数列
的值,又如数列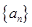 是等比数列,则可由假设推出
是等比数列,则可由假设推出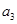 的表达式,由这两式相等可得到关于
的表达式,由这两式相等可得到关于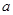 的一元二次方程,可利用
的一元二次方程,可利用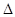 与
与 的关系来判断方程解的情况,从而确定
的关系来判断方程解的情况,从而确定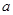 是否存在.
是否存在.试题解析:解:(1)
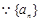 是等差数列,
是等差数列,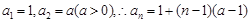 . 2分
. 2分又
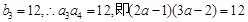 ,解得
,解得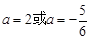 ,
,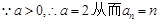 . 6分
. 6分(2)数列
 不能为等比数列. 8分
不能为等比数列. 8分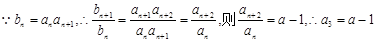 , 10分
, 10分假设数列
 能为等比数列,由
能为等比数列,由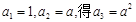 , 12分
, 12分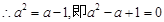 ,
,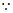 此方程无解,
此方程无解, 数列
数列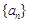 一定不能为等比数列. 14分
一定不能为等比数列. 14分
练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
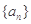 的前
的前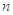 项和为
项和为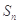 ,且
,且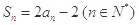 ,数列
,数列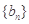 满足
满足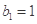 ,且点
,且点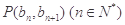 在直线
在直线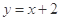 上.
上.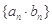 的前
的前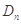 .
.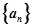 的前n项和为
的前n项和为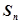 ,且
,且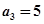 ,
,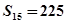 .
. 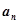 ;(2)设
;(2)设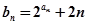 ,求数列
,求数列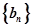 的前n项和
的前n项和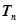 .
. 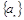 的前
的前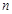 项和为
项和为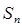 .且
.且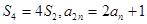
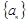 的通项公式;
的通项公式;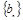 满足:
满足: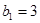 ,
,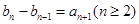 ,求数列
,求数列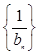 的前
的前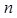 项和
项和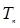 .
.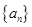 满足
满足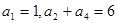 ,且对任意
,且对任意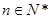 ,函数
,函数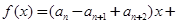
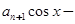
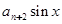 满足
满足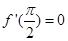 ,若
,若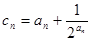 ,则数列
,则数列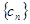 的前
的前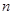 项和
项和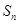 为( )
为( )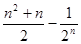
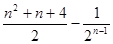
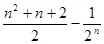
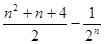
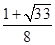
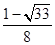
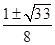
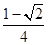
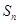 是公差不为0的等差数列
是公差不为0的等差数列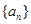 的前
的前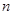 项和,若
项和,若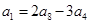 ,则
,则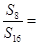 ( )
( )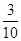
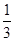
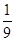
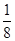
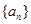 是公差不为0的等差数列,且
是公差不为0的等差数列,且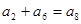 ,则
,则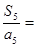 .
.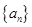 的前n项和为
的前n项和为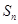 ,且
,且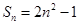 ,则
,则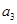 等于( )
等于( )