题目内容
已知函数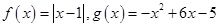 .
.
(1)若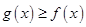 ,求实数x的取值范围;
,求实数x的取值范围;
(2)求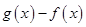 的最大值.
的最大值.
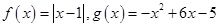 .
.(1)若
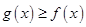 ,求实数x的取值范围;
,求实数x的取值范围;(2)求
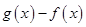 的最大值.
的最大值.(1)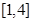 ;(2)
;(2)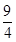 .
.
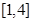 ;(2)
;(2)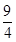 .
.试题分析:(1)本题实质就是解不等式,
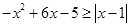 ,当然这是含绝对值的不等式,因此我们应该根据绝对值的定义,按照绝对值符号里面的式子
,当然这是含绝对值的不等式,因此我们应该根据绝对值的定义,按照绝对值符号里面的式子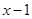 的正负性分类讨论,变为解两个二次不等式,最后还要把两个不等式的解集合并(即求并集),才能得到我们所要的结果;(2)本题实质就是求新函数
的正负性分类讨论,变为解两个二次不等式,最后还要把两个不等式的解集合并(即求并集),才能得到我们所要的结果;(2)本题实质就是求新函数 的最大值,同样由于式子中含有绝对值符号,因此我们按照绝对值符号里面的式子
的最大值,同样由于式子中含有绝对值符号,因此我们按照绝对值符号里面的式子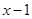 的正负性分类讨论去掉绝对值符号,变成求两个二次函数在相应区间上的最大值,最后在两个最大值中取最大的一个就是我们所要求的最大值;当然这题我们可以借助于(1)的结论,最大值一定在(1)中解集区间里取得,从而可以避免再去分类讨论,从而简化它的过程.
的正负性分类讨论去掉绝对值符号,变成求两个二次函数在相应区间上的最大值,最后在两个最大值中取最大的一个就是我们所要求的最大值;当然这题我们可以借助于(1)的结论,最大值一定在(1)中解集区间里取得,从而可以避免再去分类讨论,从而简化它的过程.试题解析:(1)当
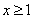 时,
时,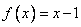 1分
1分由
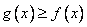 ,得
,得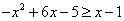 ,
,整理得
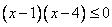 ,所以
,所以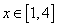 ; 3分
; 3分当
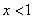 时,
时,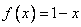 , 4分
, 4分由
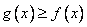 ,得
,得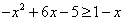 ,
,整理得
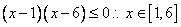 ,由
,由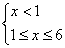 得
得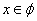 6分
6分综上
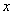 的取值范围是
的取值范围是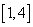 ; 7分
; 7分(2)由(1)知,
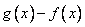 的最大值必在
的最大值必在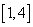 上取到, 9分
上取到, 9分所以

所以当
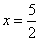 时,
时,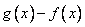 取到最大值为
取到最大值为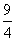 . 14分
. 14分
练习册系列答案
相关题目
 满足
满足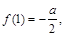 且
且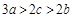 .
.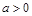 ,并求
,并求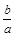 的取值范围;
的取值范围;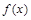 在
在 内至少有一个零点;
内至少有一个零点;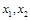 是函数
是函数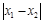 的取值范围.
的取值范围. 是定义在(-1,1)上的奇函数,其中
是定义在(-1,1)上的奇函数,其中 ,a为正整数,且满足
,a为正整数,且满足 .
. 的解析式;
的解析式; 的
的 的范围;
的范围;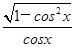 ( ).
( ). 上递增
上递增 上递增,在
上递增,在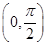 上递减
上递减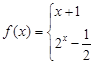
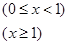 ,设
,设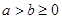 ,若
,若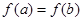 ,
,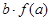 的取值范围是( )
的取值范围是( )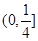
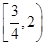
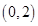
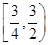
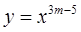 ,其中
,其中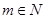 ,且在
,且在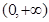 上是减函数,又
上是减函数,又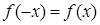 ,则
,则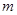 =( )
=( ) ,对于给定的正数
,对于给定的正数 ,定义函数
,定义函数 若对于函数
若对于函数 ,恒有
,恒有 ,则( )
,则( )
 的函数
的函数 图象上两点
图象上两点 是
是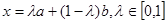 .已知向量
.已知向量 ,若不等式
,若不等式 对任意
对任意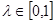 恒成立,则称函数
恒成立,则称函数 在
在 在
在 上“k阶线性近似”,则实数的k取值范围为( )
上“k阶线性近似”,则实数的k取值范围为( ) 

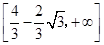

 在区间
在区间 上是减函数,则
上是减函数,则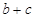 的最大值为 .
的最大值为 .