题目内容
已知AD是△ABC中BC边上的高,若AD2=BD•CD,则△ABC的形状是 .
【答案】分析:分点D在线段BC上和点D在线段BC延长线上两种情况加以讨论,结合三角形相似的知识进行证明,可得△ABC是直角三角形或钝角三角形.
解答:解:(1)若点D在线段BC上,如图(1)所示
∵AD2=BD•CD,可得
∴Rt△ABD∽Rt△CAD,可得∠BAC=∠BAD+∠CAD=∠BAD+∠B=90°
因此,△ABC是直角三角形

(2)若点D在线段BC延长线上,如图(2)所示
由(1)知仍然可证出Rt△ABD∽Rt△CAD,但此时△ABC是钝角三角形
综上所述,△ABC是直角三角形或钝角三角形
故答案为:直角三角形或钝角三角形
点评:本题给出△ABC的BC边上高AD满足AD2=BD•CD,判断三角形ABC的形状,着重考查了三角形相似的判定、直角三角形的判断等知识,属于中档题.
解答:解:(1)若点D在线段BC上,如图(1)所示
∵AD2=BD•CD,可得

∴Rt△ABD∽Rt△CAD,可得∠BAC=∠BAD+∠CAD=∠BAD+∠B=90°
因此,△ABC是直角三角形

(2)若点D在线段BC延长线上,如图(2)所示
由(1)知仍然可证出Rt△ABD∽Rt△CAD,但此时△ABC是钝角三角形
综上所述,△ABC是直角三角形或钝角三角形
故答案为:直角三角形或钝角三角形
点评:本题给出△ABC的BC边上高AD满足AD2=BD•CD,判断三角形ABC的形状,着重考查了三角形相似的判定、直角三角形的判断等知识,属于中档题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
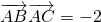 ,求
,求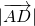 的最小值.
的最小值.