题目内容
在△ABC中,∠A=120°
(Ⅰ)若三边长构成公差为4的等差数列,求△ABC的面积;
(Ⅱ)已知AD是△ABC的中线,若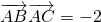 ,求
,求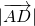 的最小值.
的最小值.
解:(Ⅰ)由题意,设三边为a,a-4,a-8(a>8),--------------(1分)
∵∠A=120°,
∴由余弦定理:a2=(a-4)2+(a-8)2-2(a-4)(a-8)cos120°---------------(2分)
即a2-18a+56=0------------------------(3分)
∴a=14或a=4(舍去)--------------------------------(4分)
∴三边为14,10,6
∴△ABC的面积为 AB×AC×sinA=
AB×AC×sinA=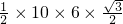 =15
=15 -----------------(6分)
-----------------(6分)
(Ⅱ)∵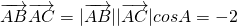 ,∠A=120°,----------------------(7分)
,∠A=120°,----------------------(7分)
∴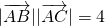 ----------------------------------(8分)
----------------------------------(8分)
∵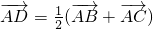 ,
,
∴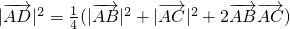 =
=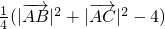
≥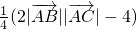 =1---------------(10分)
=1---------------(10分)
∴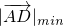 =1----------------------------------(12分)
=1----------------------------------(12分)
分析:(Ⅰ)设出三角形三边,利用余弦定理求出三边,即可得到△ABC的面积;
(Ⅱ)利用向量的数量积公式,及三角形中线向量的表示,利用基本不等式,即可求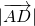 的最小值.
的最小值.
点评:本题考查余弦定理,考查向量知识,考查基本不等式,考查学生的计算能力,属于中档题.
∵∠A=120°,
∴由余弦定理:a2=(a-4)2+(a-8)2-2(a-4)(a-8)cos120°---------------(2分)
即a2-18a+56=0------------------------(3分)
∴a=14或a=4(舍去)--------------------------------(4分)
∴三边为14,10,6
∴△ABC的面积为
 AB×AC×sinA=
AB×AC×sinA=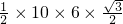 =15
=15 -----------------(6分)
-----------------(6分)(Ⅱ)∵
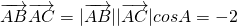 ,∠A=120°,----------------------(7分)
,∠A=120°,----------------------(7分)∴
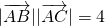 ----------------------------------(8分)
----------------------------------(8分)∵
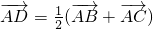 ,
,∴
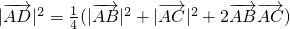 =
=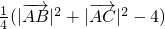
≥
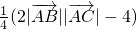 =1---------------(10分)
=1---------------(10分)∴
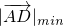 =1----------------------------------(12分)
=1----------------------------------(12分)分析:(Ⅰ)设出三角形三边,利用余弦定理求出三边,即可得到△ABC的面积;
(Ⅱ)利用向量的数量积公式,及三角形中线向量的表示,利用基本不等式,即可求
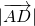 的最小值.
的最小值.点评:本题考查余弦定理,考查向量知识,考查基本不等式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目