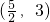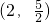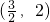Question

设关于x的方程lnx+2x-6=0的实数解为x₀，则x₀所在的区间是（　　）

A．( 5 2 ，3)

B．（3，4）

C．(2， 5 2 )

D．( 3 2 ，2)

Answer 1

令f（x）=lnx+2x-6，可知函数f（x）在区间（0，+∞）单调递增，因此函数f（x）至多有一个零点．
又f(

5

2

)=ln

5

2

+2×

5

2

-6=ln

5

2

-1＜lne-1=0，f（3）=ln3+2×3-6=ln3＞0，
∴f(

5

2

)f(3)＜0，由函数零点的判定定理可知：函数f（x）在区间(

5

2

，3)内存在零点．
综上可知：函数f（x）的唯一的一个零点在区间(

5

2

，3)内．
故选A．