题目内容
设 的内角
的内角 所对的边分别为
所对的边分别为 ,若三边的长为连续的三个正整数,且
,若三边的长为连续的三个正整数,且 ,
, ,则
,则 =( )
=( )
| A.4:3:2 | B.5:6:7 | C.5:4:3 | D.6:5:4 |
D
解析试题分析:我们知道三角形中大角对大边,因为A>B>C所以 ,又因为三边是连续的整数所以不妨设
,又因为三边是连续的整数所以不妨设 在利用余弦定理将角转化成边
在利用余弦定理将角转化成边 将
将 代入可得
代入可得
 由正弦定理知,
由正弦定理知, 所以答案为D.
所以答案为D.
考点:正弦定理、余弦定理

练习册系列答案
相关题目
已知O是平面上的一定点,A,B,C是平面上不共线的三点,动点P满足 ,
, ,则动点P的轨迹一定通过
,则动点P的轨迹一定通过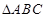 的( )
的( )
| A.重心 | B.垂心 | C.外心 | D.内心 |
 的内角
的内角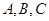 的对边分别为
的对边分别为 .若
.若 成等比数列,且
成等比数列,且 ,则
,则 ( )
( )
A. | B. | C. | D. |
在△ABC中,角A,B,C的对边为 ,若
,若 ,则角A= ( )
,则角A= ( )
| A.30° | B.30°或105° | C.60° | D.60°或120° |
在△ABC中,AC=7,∠B= ,△ABC的面积S=
,△ABC的面积S= ,则AB=
,则AB=
| A.5或3 | B.5 | C.3 | D.5或6 |
在 中,
中, 则
则 边上的高等于( )
边上的高等于( )
A. | B. | C. | D. |
在△ABC中,内角A,B,C的对边分别是a,b,c,若 ,
, ,则A=( ).
,则A=( ).
A. | B. | C. | D. |
如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100米到达B处,又测得C对于山坡的斜度为45°,若CD=50米,山坡对于地平面的坡角为θ,则cos θ=( ).
A. | B.2- |
C. -1 -1 | D. |
一船自西向东匀速航行上午10时到达一座灯塔P的南偏西75°距塔68海里的M处,下午2时到达这座灯塔的东南方向的N处,则这只船航行的速度为 ( )
A.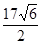 海里/小时 海里/小时 | B.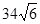 海里/小时 海里/小时 |
C.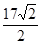 海里/小时 海里/小时 | D.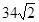 海里/小时 海里/小时 |