在△ABC中.内角A,B,C的对边分别是a,b,c.若..则A=.A． B． C． D．题目和参考答案——青夏教育精英家教网—

题目内容

在△ABC中，内角A,B,C的对边分别是a,b,c，若，，则A=（）.

A．

B．

C．

D．

解析试题分析：由由正弦定理得，则cosA=
=，∴A=30⁰，选A.
考点：正弦定理.

练习册系列答案

相关题目

设的内角所对的边分别为，若三边的长为连续的三个正整数，且，，则=( )

在中，角所对的边分别为，若，，则 ( )

设△ABC的内角A、B、C所对的边分别为a，b，c，若sinB+sinC=2sinA，3a=5c，则角B=（）
A. 60 B. 90 C. 120 D.150

在中，若，则（）

设△ABC的内角A,B,C的对边分别为若,则△ABC的形状是（）

在△ABC中，∠A=60°,a=,b=2,满足条件的△ABC（）

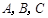设的内角所对的边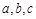成等比数列，则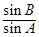的取值范围是（）

A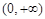．	B．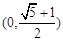
C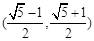．	D．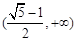

已知点

A．	B．
C．	D．

试题分类