题目内容
如图，矩形ABCD和梯形BEFC所在平面互相垂直，BE∥CF且BE＜CF，∠BCF=
，AD=
，EF=2．
（1）求证：AE∥平面DCF；
（2）设
=λ(λ＞0)，当λ取何值时，二面角A-EF-C的大小为
？
| π |
| 2 |
| 3 |
（1）求证：AE∥平面DCF；
（2）设
| AB |
| BE |
| π |
| 3 |
（1）BE∥CF，AB∥CD且BE∩AB=B，FC∩CD=C，∴面ABE∥面CDF
又AE?面ABE，∴AE∥面CDF
（2）∵∠BCF=
，且面ABCD⊥面BEFC，∴FC⊥面ABCD
以C为坐标原点，以CB，CD，CF分别为x，y，z轴建系，设BE=m，由
=λ得AB=λm，
∴A(
，λm，0)，E(
，0，m)，F(0，0，m+1)，D(0，λm，0)
平面AFE法向量
=(λ，
λ)，又∵CD⊥面CEF
∴
=(0，λm，0)是平面CEF的一个法向量，
∴cos
=
，即λ=
又AE?面ABE，∴AE∥面CDF
（2）∵∠BCF=
| π |
| 2 |
以C为坐标原点，以CB，CD，CF分别为x，y，z轴建系，设BE=m，由
| AE |
| BE |
∴A(
| 3 |
| 3 |
平面AFE法向量
| n |
| 3 |
| 3 |
∴
| CD |
∴cos
| π |
| 3 |
|
| ||||
|
|
| 3 |
| 2 |
练习册系列答案
相关题目
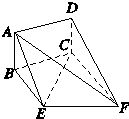如图，矩形ABCD和梯形BEFC所在平面互相垂直，∠BCF=∠CEF=90°，AD=
如图，矩形ABCD和梯形BEFC所在的平面互相垂直，BE∥CF，BE＜CF，∠BCF=
如图，矩形ABCD和矩形BCEF所在平面互相垂直，G为边BF上一点，∠CGE=90°，
如图，矩形ABCD和直角梯形BEFC所在平面互相垂直，∠BCF=90°，BE∥CF，CE⊥EF，AD=
如图，矩形ABCD和直角梯形BEFC所在平面互相垂直，∠BCF=90°，BE∥CF，CE⊥EF，AD=