题目内容
 如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=
如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=| 3 |
(1)求异面直线AD与EF所成的角;
(2)当二面角D-EF-B的大小为45°时,求二面角A-EC-F的大小.
分析:方法一:(1)作EM⊥CF于M,则易知为异面直线AD与EF所成的角,在在RT△EMF中求解.
(2)∠DEC 为二面角D-EF-B的平面角.作BN⊥CE于N,则∠ANB即为二面角A-EC-F的平面角的补角
方法二:(1)以点C为坐标原点,以CB,CF和CD分别为作x轴,y轴和z轴,建立空间直角坐标系,利用
,
夹角求出异面直线AD与EF所成的角
(2)利用面ECA的一个法向量与面ECF的一个法向量夹角求出二面角A-EC-F的大小.
(2)∠DEC 为二面角D-EF-B的平面角.作BN⊥CE于N,则∠ANB即为二面角A-EC-F的平面角的补角
方法二:(1)以点C为坐标原点,以CB,CF和CD分别为作x轴,y轴和z轴,建立空间直角坐标系,利用
| DA |
| FE |
(2)利用面ECA的一个法向量与面ECF的一个法向量夹角求出二面角A-EC-F的大小.
解答: 解:(方法一)(1)作EM⊥CF于M,则EM∥BC∥AD,
解:(方法一)(1)作EM⊥CF于M,则EM∥BC∥AD,
在RT△EMF中,易知四边形BCME为矩形,所以EM=BC=AD=
,又EF=2
所以cos∠MEF=
=
,∠MEF=30°,即异面直线AD与EF所成的角为30°.…(5分)
(2)矩形ABCD和直角梯形BEFC所在平面互相垂直,∴DC⊥EF,又CE⊥EF,
即∠DEC为二面角D-EF-B的平面角,即∠DEC=45°.
若设EC=x,则在直角三角形CEF中,CE•EF=CF•EM,x•2=
•
,x=2
.
∴CE=CD=AB=2
.
作BN⊥CE于N,则∠ANB即为二面角A-EC-F的平面角的补角,

在直角三角形CBE中,CB•BE=CE•BN,且BE=
=3,解得BN=
,
∴tan∠ANB=
=
,
∴二面角A-EC-F的大小为π-arctan
.…(12分)
(方法二)
如图,以点C为坐标原点,以CB,CF和CD分别为作x轴,y轴和z轴,建立空间直角坐标系 C-xyz.…(1分)
F(0,c,0),D(0,0,a)…(2分)
(1)
=(
,0,0),
=(
,0,0),
=(
,b-c,0),
由|
|=2,得3+(b-c)2=4,∴b-c=-1.所以
=(
,-1,0).
所以cos<
,
>=
=
=
,…(4分)
所以异面直线AD与EF成30° …(5分)
(2)当二面角D-EF-B的大小为45,即∠DEC=45°.
设
=(1,y,z)为平面AEC的法向量,则
•
=0,
•
=0,求得
=(1,-
,-
).…(8分)
又因为BA⊥平面BEFC,
=(0,0,1),所以cos<
,
>
=-
…(10分)
因为二面角A-EC-F是锐二面角,
所以二面角A-EC-F的大小为π-arccos
…(12分)
 解:(方法一)(1)作EM⊥CF于M,则EM∥BC∥AD,
解:(方法一)(1)作EM⊥CF于M,则EM∥BC∥AD,在RT△EMF中,易知四边形BCME为矩形,所以EM=BC=AD=
| 3 |
所以cos∠MEF=
| EM |
| EF |
| ||
| 2 |
(2)矩形ABCD和直角梯形BEFC所在平面互相垂直,∴DC⊥EF,又CE⊥EF,
即∠DEC为二面角D-EF-B的平面角,即∠DEC=45°.
若设EC=x,则在直角三角形CEF中,CE•EF=CF•EM,x•2=
| x2+22 |
| 3 |
| 3 |
∴CE=CD=AB=2
| 3 |
作BN⊥CE于N,则∠ANB即为二面角A-EC-F的平面角的补角,

在直角三角形CBE中,CB•BE=CE•BN,且BE=
| EC2-BC2 |
| 3 |
| 2 |
∴tan∠ANB=
| AB |
| BN |
4
| ||
| 3 |
∴二面角A-EC-F的大小为π-arctan
4
| ||
| 3 |
(方法二)
如图,以点C为坐标原点,以CB,CF和CD分别为作x轴,y轴和z轴,建立空间直角坐标系 C-xyz.…(1分)
|
(1)
| DA |
| 3 |
| CB |
| 3 |
| FE |
| 3 |
由|
| FE |
| FE |
| 3 |
所以cos<
| DA |
| FE |
| ||||
|
|
| 3 | ||
|
| ||
| 2 |
所以异面直线AD与EF成30° …(5分)
(2)当二面角D-EF-B的大小为45,即∠DEC=45°.
设
| n |
| n |
| AE |
| n |
| EC |
| n |
| ||
| 3 |
| 1 |
| 2 |
又因为BA⊥平面BEFC,
| BA |
| n |
| BA |
| ||||
|
|
| ||
| 19 |
因为二面角A-EC-F是锐二面角,
所以二面角A-EC-F的大小为π-arccos
| ||
| 19 |
点评:本题考查空间直线、平面位置关系的判断,二面角大小求解,考查空间想象能力、推理论证、计算、转化能力.利用向量这一工具,解决空间几何体问题,能够降低思维难度.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
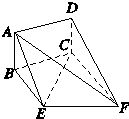 如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD=
如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD= 如图,矩形ABCD和梯形BEFC所在的平面互相垂直,BE∥CF,BE<CF,∠BCF=
如图,矩形ABCD和梯形BEFC所在的平面互相垂直,BE∥CF,BE<CF,∠BCF= 如图,矩形ABCD和矩形BCEF所在平面互相垂直,G为边BF上一点,∠CGE=90°,
如图,矩形ABCD和矩形BCEF所在平面互相垂直,G为边BF上一点,∠CGE=90°, 如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=
如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=