Question

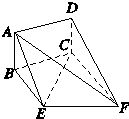
如图，矩形ABCD和梯形BEFC所在的平面互相垂直，BE∥CF，BE＜CF，∠BCF=

π

2

，AD=

3

，EF=2．
（I）求证：DF∥平面ABE；
（II）设

CF

CD

=λ，问：当λ取何值时，二面角D-EF-C的大小为

π

6

．

Answer 1

分析：（1）根据在一个平面上有两条相交直线与另一个平面的两条相交直线平行，得到两个平面平行，根据面面平行再推出线面平行．
（2）建立坐标系，求出平面DEF的一个法向量和平面CEF的一个法向量，代入向量夹角公式，根据二面角D-EF-C的大小为

π

6

，易构造一个关于λ的方程，解方程即可得到λ的值．

解答：证明：（I）BE∥CF，AB∥CD且BE∩AB=B，FC∩CD=C，…2分
∴面ABE∥面CDF…3分，
又DF?面CDF，
DF∥平面ABE；…4分
解：（II）过E作GE⊥CF交CF于G
∴EG∥BC∥AD且EG=BC=AD
∴EG=AD=

3

，又EF=2，
∴GF=1
∵四边形ABCD为科技，
∴DC⊥BC
∵∠BCF=

π

2

，∴FC⊥BC
又平面AC⊥平面BF，平面AC∩平面BF=BC
∴FC⊥平面AC，
∴FC⊥D
以C为坐标原点，以CB，CD，CF分别为x，y，z轴建系，…6分
设CD=m，CF=λm
A(

3

，m，0)，E(

3

，0，λm-1)，F(0，0，λm)，D(0，m，0)，B（

3

，0，0），C（0，0，0）
∴

EF

=（-

3

，0，1），

DF

=（0，-m，λm）…7分
取平面CEF的一个法向量

n

=（0，1，0）…8分
取平面DEF的一个法向量

m

=（x，y，z），则

m • EF =0 m • DF =0

，即

- 3 x+z=0 -my+λmz=0

则

m

=（1，

3

λ，

3

）…10分
则cos

π

6

=

3 λ

4+3λ2

=

3

2

…12分
解得：λ=2
即当λ=2时，二面角D-EF-C的大小为

π

6

…13分

点评：本题考查用空间向量求两个平面间的夹角，本题解题的关键是求出两个平面的法向量，把解题的重点转移到数字的运算．