题目内容
(本题满分13分)已知 与两平行直线
与两平行直线 都相切,且圆心
都相切,且圆心 在直线
在直线 上,
上,
(Ⅰ)求 的方程;
的方程;
(Ⅱ)斜率为2的直线 与
与 相交于
相交于 两点,
两点,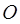 为坐标原点且满足
为坐标原点且满足 ,求直线
,求直线 的方程。
的方程。
(1) ;(2)
;(2) 。
。
解析试题分析:(1)由题意知 的直径为两平行线
的直径为两平行线  之间的距离
之间的距离
∴ 解得
解得 ,…………………………………3分
,…………………………………3分
由圆心 到
到  的距离
的距离 得
得 ,检验得
,检验得 ………6分
………6分
∴ 的方程为
的方程为 ………………………………………7分
………………………………………7分
(2)由(1)知 过原点,若
过原点,若 ,则
,则 经过圆心,…………… 9分
经过圆心,…………… 9分
易得 方程:
方程: …………………………13分
…………………………13分
(注:其它解法请参照给分.)
考点:本题主要考查圆的标准方程,直线与圆相交的位置关系,直线的点斜式方程,圆的几何性质,点到直线的距离公式。
点评:中档题,当直线与圆相交时,常常根据垂径定理由垂直得中点,进而由弦长的一半,圆的半径及弦心距构造直角三角形,利用勾股定理来解答。

练习册系列答案
相关题目
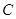 经过坐标原点和点
经过坐标原点和点 ,且与直线
,且与直线 相切, 从圆
相切, 从圆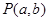 向该圆引切线
向该圆引切线 ,
, 为切点,
为切点,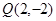 ,且
,且 , 试判断点
, 试判断点 是否总在某一定直线
是否总在某一定直线 上,若是,求出
上,若是,求出 轴的交点为
轴的交点为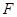 ,点
,点 是直线
是直线 上两动点,且以
上两动点,且以 过点
过点 截直线
截直线 的弦长为
的弦长为 ;
; 的值;
的值;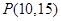 的圆的切线所在的直线方程.
的圆的切线所在的直线方程. ,圆心在直线
,圆心在直线 上,且被直线
上,且被直线 截得的弦长为
截得的弦长为 ,求圆C的方程
,求圆C的方程 ,直线
,直线 以及
以及 上一点
上一点 .
.
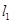 上且与直线
上且与直线 的圆⊙M的方程.
的圆⊙M的方程. 分别与直线
分别与直线 、圆⊙依次相交于A、B、C三点,
、圆⊙依次相交于A、B、C三点, .
.  上,且经过圆
上,且经过圆 与圆
与圆 的交点的圆方程.
的交点的圆方程. 与圆
与圆 相交于
相交于 两点,
两点, 的取值范围;
的取值范围; 为坐标原点,且
为坐标原点,且 ,求
,求