题目内容
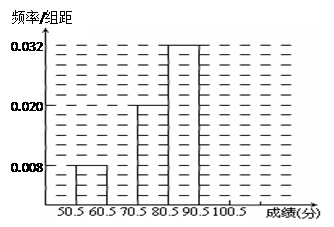
(本小题满分12分)为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 6 | 0.08 |
| 60.5~70.5 | | 0.16 |
| 70.5~80.5 | 15 | |
| 80.5~90.5 | 24 | 0.32 |
| 90.5~100.5 | | |
| 合计 | 75 | |
(Ⅰ)填充频率分布表的空格(将答案直接填在答题卡的表格内);
(Ⅱ)补全频率分布直方图;
(Ⅲ)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
(Ⅰ)
分组频数 频率 50.5~60.5 6 0.08 60.5~70.5 12 0.16 70.5~80.5 15 0.20 80.5~90.5 24 0.32 90.5~100.5 18 0.24 合计 75 1.00
(Ⅱ)
(Ⅲ)208人。
解析试题分析:
分组频数 频率 50.5~60.5 6 0.08 60.5~70.5 12 0.16 70.5~80.5 15 0.20 80.5~90.5 24 0.32 90.5~100.5 18 0.24 合计 75 1.00
(Ⅱ) 频率分布直方图如下所示 
(Ⅲ)该校获得二等奖的学生约为0.26´800=208(人)
考点:频率分布表;频率分布直方图。
点评:在频率分布直方图中,小长方体的面积就是这组数据的频率。属于基础题型。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
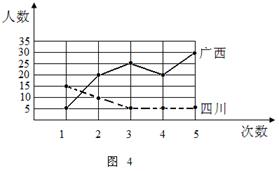
某车间为了规定工时额,需确定加工零件所花费的时间,为此做了4次试验,得到的数据如下图:若加工时间 与零件个数
与零件个数 之间有较好的线性相关关系。(
之间有较好的线性相关关系。(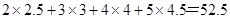 )
)
 | 2 | 3 | 4 | 5 |
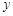 | 2.5 | 3 | 4 | 4.5 |
(1)求加工时间与零件个数的线性回归方程;
(2)试预报加工10个零件需要的时间。
(附:回归方程系数公式
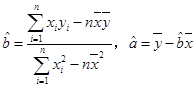 )
) (本小题满分10分)国家有甲,乙两个射击队,若两个队共进行了8次热身赛,
各队的总成绩见下表:
| 甲队 | 403 | 390 | 397 | 404 | 388 | 400 | 412 | 406 |
| 乙队 | 417 | 401 | 410 | 416 | 406 | 421 | 398 | 411 |
分别求两个队总成绩的样本平均数和样本方差,根据计算结果,若选一个代表队参加奥运会比赛,你认为应该选哪一个队?
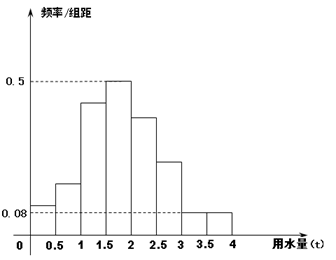
 户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图).
户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图).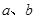 的值,并估计该社区家庭月均用水量不超过
的值,并估计该社区家庭月均用水量不超过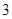 吨的频率;
吨的频率; 、
、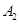 、
、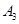 是户月均用水量为
是户月均用水量为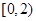 的居民代表,
的居民代表, 、
、 是户月均用水量为
是户月均用水量为 的居民代表. 现从这五位居民代表中任选两人参加水价论证会,请列举出所有不同的选法,并求居民代表
的居民代表. 现从这五位居民代表中任选两人参加水价论证会,请列举出所有不同的选法,并求居民代表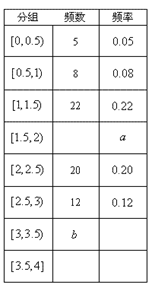
 ,
, ,…,
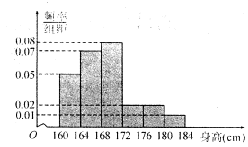
,…, 后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题:
 ,求
,求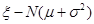 .则
.则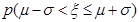 =0.6826,
=0.6826,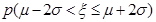 ="0.9544,"
="0.9544," 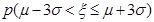 =0.9974.
=0.9974.

 的值;
的值;