题目内容
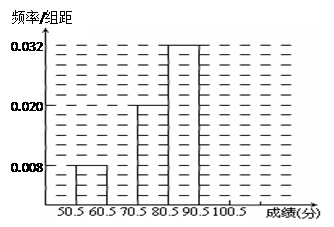
(本题满分13分)某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中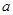 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比
如下表所示,求数学成绩在[50,90)之外的人数.
| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x∶y | 1∶1 | 2∶1 | 3∶4 | 4∶5 |
(1)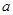 =0.005 (2)73 (3)10
=0.005 (2)73 (3)10
解析试题分析:(1)由频率分布直方图可知
(0.04+0.03+0.02+2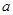 )×10=1.
)×10=1.
所以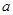 =0.005. ……4分
=0.005. ……4分
(2)该100名学生的语文成绩的平均分约为 =0.05×55+0.4×65+0.3×75+0.2×85+0.05×95=73. ……8分
=0.05×55+0.4×65+0.3×75+0.2×85+0.05×95=73. ……8分
(3)由频率分布直方图及已知的语文成绩、数学成绩分布在各分数段的人数比,
可得下表:
于是数学成绩在[50,90)之外的人数为100-(5+20+40+25)=10. ……13分分数段 [50,60) [60,70) [70,80) [80,90) x 5 40 30 20 x∶y 1∶1 2∶1 3∶4 4∶5 y 5 20 40 25
考点:本小题主要考查频率分布直方图的读图识图问题和根据频率分布直方图计算平均数等问题,考查学生分析问题、解决问题的能力和运算求解能力.
点评:读频率分布直方图,要明确频率分布直方图的意义,即图中的每一个小矩形的面积是数据落在该区间上的频率,所以小矩形的面积之和为1.

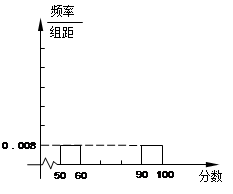
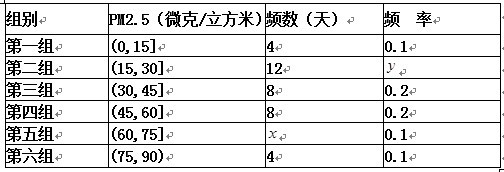
(本小题满分12分)为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 6 | 0.08 |
| 60.5~70.5 | | 0.16 |
| 70.5~80.5 | 15 | |
| 80.5~90.5 | 24 | 0.32 |
| 90.5~100.5 | | |
| 合计 | 75 | |
(Ⅰ)填充频率分布表的空格(将答案直接填在答题卡的表格内);
(Ⅱ)补全频率分布直方图;
(Ⅲ)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?

 ,
, 之间的矩形的高,并完成直方图;
之间的矩形的高,并完成直方图;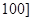 之间任取两份进行分析,在抽取的结果中,求至少有一份分数在
之间任取两份进行分析,在抽取的结果中,求至少有一份分数在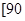 ,
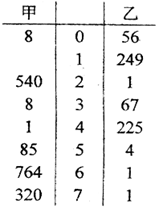
, (1)求季军队中男运动员的人数(2)从前排就座的亚军队5人(3男2女)中随机抽取2人上台领奖请列出所有的基本事件,并求亚军队中有女生上台领奖的概率;
(1)求季军队中男运动员的人数(2)从前排就座的亚军队5人(3男2女)中随机抽取2人上台领奖请列出所有的基本事件,并求亚军队中有女生上台领奖的概率;

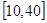 间的频率是多少?
间的频率是多少? 和
和 房屋的面积
房屋的面积 的数据:
的数据: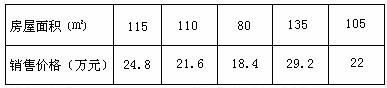
 归方程。(保留四位小数)
归方程。(保留四位小数)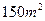 时的销售价格。
时的销售价格。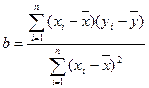 ,
,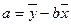
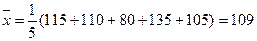 ,
,
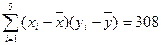 ,
,
 后,画出如下部分频率分布直方图。观察图形,回答下列问题:
后,画出如下部分频率分布直方图。观察图形,回答下列问题: