题目内容
| OP |
| OA |
| ||
|
|
| ||
|
|
分析:根据题中向量等式,化简可得
=λ(
+
)=λ
,其中
是与
、
方向相同的单位向量之和,点P在射线AF上运动.由向量加法的平行四边形法则可得AF平分∠BAC,所以点P的轨迹为∠BAC的平分线,从而得到△ABC的内心在点P的轨迹上,可得答案.
| AP |
| ||
|
|
| ||
|
|
| AF |
| AF |
| AB |
| AC |
解答:解:∵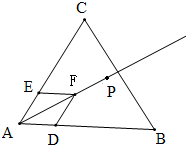
、
分别表示与向量
、
方向相同的单位向量,
∴设
=
、
=
,则
=
=1,
以AD、AE为邻边作平行四边形ADFE,可得
=
+
=
+
,
∴四边形ADFE是菱形,可得AF平分∠BAC.
又∵
=
+λ(
+
),λ∈[0,+∞),
∴
=
-
=λ(
+
)=λ
,可得点P在射线AF上运动.
由于△ABC的内心在∠BAC的平分线上,所以点P的轨迹一定经过△ABC的内心.
故选:B

| ||
|
|
| ||
|
|
| AB |
| AC |
∴设
| AD |
| ||
|
|
| AE |
| ||
|
|
| |AD| |
| |AE| |
以AD、AE为邻边作平行四边形ADFE,可得
| AF |
| AD |
| AE |
| ||
|
|
| ||
|
|
∴四边形ADFE是菱形,可得AF平分∠BAC.
又∵
| OP |
| OA |
| ||
|
|
| ||
|
|
∴
| AP |
| OP |
| OA |
| ||
|
|
| ||
|
|
| AF |
由于△ABC的内心在∠BAC的平分线上,所以点P的轨迹一定经过△ABC的内心.
故选:B
点评:本题给出三角形中的点P满足的向量等式,求P的轨迹经过三角形的哪一个心.着重考查了向量的加法法则、向量共线的条件和三角形的“五心”等知识,属于中档题.

练习册系列答案
相关题目