题目内容
O是平面α上一点,A、B、C是平面α上不共线三点,平面α内的动点P满足| OP |
| OA |
| AB |
| AC |
| 1 |
| 2 |
| PA |
| PB |
| PC |
分析:把已知的等式进行等价变形得
=
,故有
+
=
,代入所求的式子进行化简.
| BP |
| PC |
| PC |
| PB |
| 0 |
解答:解:∵动点P满足
=
+λ(
+
),∴
=λ (
+
)=
(
+
),
∴2
=
+
,
-
=
-
,
=
,
∴
+
=
,∴
•(
+
)=
•
=0,
故答案为:0.
| OP |
| OA |
| AB |
| AC |
| AP |
| AB |
| AC |
| 1 |
| 2 |
| AB |
| AC |
∴2
| AP |
| AB |
| AC |
| AP |
| AB |
| AC |
| AP |
| BP |
| PC |
∴
| PC |
| PB |
| 0 |
| PA |
| PB |
| PC |
| PA |
| 0 |
故答案为:0.
点评:本题考查向量的加减运算,两个向量的数量积,体现了等价转化的数学思想.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
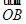 |·
|·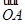 +|
+| .将它类比到平面的情形是:若O是△ABC内一点,有S△OBC·
.将它类比到平面的情形是:若O是△ABC内一点,有S△OBC· =
=