Question

已知椭圆C₁：，椭圆C₂以C₁的长轴为短轴，且与C₁有相同的离心率．
（1）求椭圆C₂的方程；
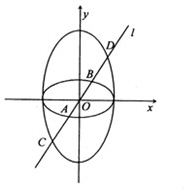
（2）设O为坐标原点，过O的直线l与C₁相交于A，B两点，且l与C₂相交于C，D两点．若|CD|=2|AB|，求直线l的方程．

Answer 1

解：（1）由题意，椭圆C₁：的长半轴长为2，离心率为，
∵椭圆C₂以C₁的长轴为短轴，
∴椭圆C₂的对称中心在原点，焦点在y轴上，
设椭圆C₂：，a＞2，
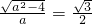∴，解得a=4，
∴椭圆C₂的方程为．
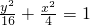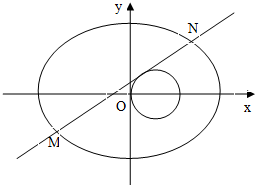
（2）如图，设直线l的方程为y=kx，或x=0（舍），
设B（x₁，y₁），D（x₂，y₂），
根据椭圆的对称性，得A（-x₁，-y₁），C（-x₂，-y₂），
则=（2x₁，2y₁），=（2x₂，2y₂），
∵|CD|=2|AB|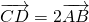，∴，∴x₂=2x₁，
由方程组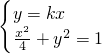，消去y，得（4k²+1）x²-4，解得，
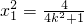同理，根据直线l与椭圆C₂的方程得=，
由x₂=2x₁，得，
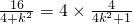解得k=±1．
∴直线l的方程为x-y=0，或x+y=0．
分析：（1）由题意，椭圆C₁：的长半轴长为2，离心率为，由椭圆C₂以C₁的长轴为短轴，知椭圆C₂的对称中心在原点，焦点在y轴上，由此能求出椭圆C₂的方程．
（2）设直线l的方程为y=kx，或x=0（舍），设B（x₁，y₁），D（x₂，y₂），根据椭圆的对称性，得A（-x₁，-y₁），C（-x₂，-y₂），则=（2x₁，2y₁），=（2x₂，2y₂），由|CD|=2|AB|，知x₂=2x₁，（4k²+1）x²-4，解得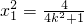，由此能求出直线l的方程．
点评：本题考查椭圆方程的求法，考查直线方程的求法，解题时要认真审题，注意等价转化思想的合理运用．