Question

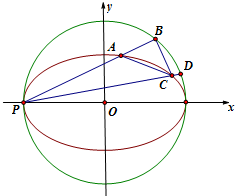已知椭圆C₁：

x2

a2

+

y2

b2

=1（a＞b＞0）和圆C₂：x²+y²=r²（r＞0）都过点P（-1，0），且椭圆C₁离心率为

2

2

，过点P作斜率为k₁，k₂的直线分别交椭圆C₁、圆C₂于点A、B、C、D（如图），k₁=2k₂．
（1）求椭圆C₁和圆C₂的方程；
（2）求证：直线BC恒过定点．

Answer 1

分析：（1）直接把定点代入圆的方程求圆的半径，利用椭圆过定点得到a的值，代入离心率后求得c的值，结合b²=a²-c²求得b的值，则圆与椭圆的方程可求；
（2）设出直线AB和CD的方程，分别和圆与椭圆联立后求出A，B，C，D的坐标，求出BC的斜率（用k₂）表示，由点斜式写出直线BC的方程后可得直线BC恒过定点．

解答：（1）解：由圆C₂：x²+y²=r²（r＞0）过点P（-1，0），得到r²=1，
所以圆C₂的方程为x²+y²=1．
由椭圆C₁离心率为e=

c

a

=

2

2

，
由椭圆C₁：

x2

a2

+

y2

b2

=1（a＞b＞0）过点P（-1，0），得

1

a2

=1，
所以a=1，代入

c

a

=

2

2

，得c=

2

2

，
所以b2=a2-c2=

1

2

．
所以椭圆C₁的方程为x²+2y²=1；
（2）证明：由题意可设直线AB的方程为y=k₁（x+1），直线CD的方程为y=k₂（x+1）．
由

x2+2y2=1 y=k1(x+1)

⇒(1+2

k

2 1

)x2+4k1x+2

k

2 1

-1=0，A(-1+

2

1+2 k 2 1

，

2k1

1+2 k 2 1

)．
由

x2+y2=1 y=k1(x+1)

⇒(1+

k

2 1

)x2+2k1x+

k

2 1

-1=0，B(-1+

2

1+ k 2 1

，

2k1

1+ k 2 1

)．
同理可得：C(-1+

2

1+2 k 2 2

，

2k2

1+2 k 2 2

)，D(-1+

2

1+ k 2 2

，

2k2

1+ k 2 2

)，
所以kBC=

2k2 1+2k22 - 2k1 1+2k12

-1+ 2 1+2k22 +1- 2 1+2k12

，因为k₁=2k₂，所以kBC=-

1

2k2

，
所以直线BC的方程为y-

2k2

1+k22

=-

1

2k2

(x+1-

2

1+k22

)．
即y=-

1

2k2

(x-1)，恒过定点（1，0）．

点评：本题考查了圆与椭圆的标准方程，考查了直线与圆锥曲线的关系，直线与圆锥曲线的关系问题，往往需要涉及繁杂的计算，这就需要学生有较强的运算能力，属难题．