题目内容
设F1、F2是椭圆E: 的左、右焦点,P为直线
的左、右焦点,P为直线 上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
A. | B. | C. | D. |
C
解析试题分析:试题分析:根据题意,由于F1、F2是椭圆E: 的左、右焦点,P为直线
的左、右焦点,P为直线 上一点,那么结合△F2PF1是底角为30°的等腰三角形,F2F1=F2P="2c,"
上一点,那么结合△F2PF1是底角为30°的等腰三角形,F2F1=F2P="2c,"  ,故可知答案为C.
,故可知答案为C.
考点:椭圆的性质
点评:主要是考查了椭圆的几何形性质的运用,属于基础题。

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
已知双曲线 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率为
的焦点重合,且双曲线的离心率为 ,则此双曲线的方程为
,则此双曲线的方程为
A. | B. | C.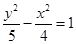 | D. |
双曲线 的渐近线方程是( )
的渐近线方程是( )
A. | B. | C. | D. |
椭圆 的离心率为 ( )
的离心率为 ( )
A. | B. | C. | D. |
已知点A(1,0)和圆 上一点P,动点Q满足
上一点P,动点Q满足 ,则点Q的轨迹方程为( )
,则点Q的轨迹方程为( )
A. | B. |
C. | D. |
曲线C: ,(
,( 为参数)的普通方程为 ( )
为参数)的普通方程为 ( )
A. | B. |
C. | D. |
 分别为双曲线
分别为双曲线 (a>0,b>0)的左、右焦点,
(a>0,b>0)的左、右焦点,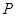 为双曲线左支上的任意一点,若
为双曲线左支上的任意一点,若 的最小值为
的最小值为 ,则双曲线离心率
,则双曲线离心率 的取值范围是 ( )
的取值范围是 ( )



 围成的区域(含边界)为Ωn(n=1,2,…),当点(x,y)分别在Ω1,Ω2,…上时,x+y的最大值分别是M1,M2,…,则
围成的区域(含边界)为Ωn(n=1,2,…),当点(x,y)分别在Ω1,Ω2,…上时,x+y的最大值分别是M1,M2,…,则 Mn=( )
Mn=( )

 是双曲线
是双曲线 的左焦点,过
的左焦点,过 且平行于双曲线渐近线的直线与圆
且平行于双曲线渐近线的直线与圆 交于点
交于点 ,且点
,且点 上,则该双曲线的离心率是( )
上,则该双曲线的离心率是( ) 


