Question

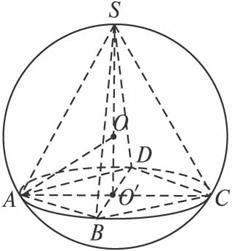
正四棱锥S—ABCD内接于一个半径为R的球，那么这个正四棱锥体积的最大值为_______________.

Answer 1

答案： R³  方法一：设底面边长为2a,球心为O，截面圆心为O′，则AO′=a,AO=R,OO′=.V_s—ABCD=×4a²×(R+).

设=t，则2a²=R²-t².∴V_s—ABCD=(R²-t²)(R+t)=(R³+R²t-t²R-t³).V_s—ABCD′

=(R²-2tR-3t²)=0，得t=时，V_s—ABCD最大，最大值为(R²-)(R+)= ××R³=R³.

方法二：V_s—ABCD=(2R-2t)(R+t)(R+t)≤R³,当且仅当2R-2t=R+t,t=R时取等号.