Question

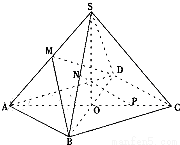
在正四棱锥S-ABCD中，点O是底面中心，SO=2，侧棱SA=2

3

，则该棱锥的体积为

32

3

．

Answer 1

分析：根据题意，利用勾股定理算出底面中心到顶点的距离为2

2

，利用正方形的性质得出底面边长为4，再由锥体的体积公式加以计算，即可得到该棱锥的体积．

解答：解：∵在正四棱锥S-ABCD中，侧棱SA=2

3

，高SO=2，
∴底面中心到顶点的距离AO=

SA2-SO2

=2

2

因此，底面正方形的边长AB=

2

AO=4，底面积S=AB²=16
该棱锥的体积为V=

1

3

S_ABCD•SO=

1

3

×16×2=

32

3

．
故答案为：

32

3

．

点评：本题给出正四棱锥的高和侧棱长，求它的体积．着重考查了正四棱锥的性质、正方形中的计算和锥体体积公式等知识，属于基础题．