Question

正四棱锥S-ABCD中，侧棱与底面所成的角为α，侧面与底面所成的角为β，侧面等腰三角形的底角为γ，相邻两侧面所成的二面角为θ，则α、β、γ、θ的大小关系是（　　）

A．α＜β＜γ＜θ

B．α＜β＜θ＜γ

C．θ＜α＜γ＜β

D．α＜γ＜β＜θ

Answer 1

分析：在正四棱锥S-ABCD，找出空间角的平面角，考虑通过三角函数的值大小关系得出角的大小关系．

解答：解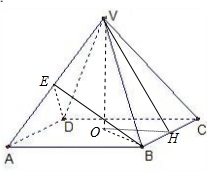：如图，正四棱锥S-ABCD，设AB=2，高VO=h．H为BC中点．
在RT△VOB中，tanα=tan∠VBO=

VO

BO

=

h

2

，
在RT△VOh中，tanβ=tan∠VHO=

VO

HO

=h，
在RT△VHC中，tanγ=tan∠VCH=

VH

CH

=

h2+1

，
∴0＜tanα＜tanβ＜tanγ．∴α＜β＜γ＜

π

2

．
过点D作DE⊥VA于E，连接ED，由于△VBA≌△VDA，∴ED⊥VA，∠BED为相邻两侧面所成的二面角θ．
S_△VAB=

1

2

VA×BE=

1

2

×BC×VH，即

1

2

h2+2

×BE=

1

2

×2×

h2+1

，BE²=

4(h2+1)

h2+2

，DE²+BE²=2DE²＜BD²，∴∠BED为钝角，
∴α＜β＜γ＜θ．
故选A．

点评：本题考查了正四棱锥的性质，空间角的定义及度量．三角函数的单调性．考查了空间想象能力、转化、计算能力．