题目内容
若函数f（x）=ax2-lnx在（0，1]上存在唯一零点，则实数a的取值范围是（ ）
| A、[0，2e] | ||
B、[0，
| ||
| C、C、（-∞，-1] | ||
| D、（-∞，0] |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：由f（x）=ax2-lnx=0，得ax2=lnx，作出函数g（x）=ax2和m（x）=lnx的图象，即可得到结论．
解答：
解：由f（x）=ax2-lnx=0，得ax2=lnx，
设g（x）=ax2和m（x）=lnx，
若a=0，则g（x）和m（x）只有一个交点，满足条件，
若a＞0，当x∈（0，1]，g（x）＞0，m（x）≤0，此时两个函数没有交点，
若a＜0，作出函数g（x）=ax2和m（x）=lnx的图象，
此时g（x）和m（x）只有一个交点，满足条件，
综上a≤0，
故选：D
解：由f（x）=ax2-lnx=0，得ax2=lnx，设g（x）=ax2和m（x）=lnx，
若a=0，则g（x）和m（x）只有一个交点，满足条件，
若a＞0，当x∈（0，1]，g（x）＞0，m（x）≤0，此时两个函数没有交点，
若a＜0，作出函数g（x）=ax2和m（x）=lnx的图象，
此时g（x）和m（x）只有一个交点，满足条件，
综上a≤0，
故选：D
点评：本题主要考查函数零点的判断和应用，根据函数零点和方程之间的关系转化为两个函数的图象问题是解决本题的关键．
练习册系列答案
相关题目
已知l，m为两条不同直线，α，β为两个不同平面，则下列命题中不正确的是（ ）
| A、若l∥α，m?α，则l∥m |
| B、若α∥β，l⊥α，则l⊥β |
| C、若α∥β，l?α，则l∥β |
| D、若α⊥β，α∩β=l，m?α，m⊥l，则m⊥β |
执行如图所示的程序框图，如果输入的x，y，N的值分别为1，2，3，则输出的S=（ ）
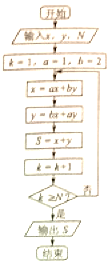
| A、27 | B、81 | C、99 | D、577 |
偶函数f（x）在[-1，0]上为减函数，A、B为某个锐角三角形的两个内角，则（ ）
| A、f（cosA）＞f（cosB） |
| B、f（sinA）＞f（sinB） |
| C、f（sinA）＞f（cosB） |
| D、f（sinA）＜f（cosB） |
若b＜0，a+b＞0，则a-b的值（ ）
| A、不能确定 | B、小于零 |
| C、等于零 | D、大于零 |