题目内容
【题目】已知抛物线![]() 和
和![]() 的焦点分别为
的焦点分别为![]() ,
, ![]() 交于O,A两点(O为坐标原点),且
交于O,A两点(O为坐标原点),且![]()
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)过点O的直线交![]() 的下半部分于点M,交
的下半部分于点M,交![]() 的左半部分于点N,点
的左半部分于点N,点![]() ,求
,求![]() 面积的最小值.
面积的最小值.
【答案】(1) ![]() (2)8
(2)8
【解析】试题分析:(1)由已知条件推导出![]() ,由
,由![]()
![]() ,解得
,解得![]() ,结合点在抛物线上得到P=2.(2)设过O的直线方程为y=kx,联立
,结合点在抛物线上得到P=2.(2)设过O的直线方程为y=kx,联立![]() ,得M(
,得M(![]() ),联立
),联立![]() ,得N(4k,4k2),由此利用点到直线的距离公式能求出△PMN面积表达式,再换元法求得函数的最值。
,得N(4k,4k2),由此利用点到直线的距离公式能求出△PMN面积表达式,再换元法求得函数的最值。
(1)设![]() ,有
,有![]() ①,由题意知,
①,由题意知, ![]() ,
, ![]() ,
,
∴![]()
∵![]()
![]() ,∴
,∴![]()
![]() ,有
,有![]() ,
,
解得![]() ,
,
将其代入①式解得![]() ,从而求得
,从而求得![]() ,
,
所以![]() 的方程为
的方程为![]() .
.
(2)联立![]() 得
得![]() ,联立
,联立![]() 得
得![]() ,
,
从而![]() ,
,
点![]() 到直线
到直线![]() 的距离
的距离![]() ,进而
,进而
![]()
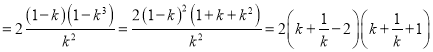 令
令![]() ,有
,有![]() ,
,
当![]() ,即
,即![]() 时,
时,
即当过原点直线为![]() 时,△
时,△![]() 面积取得最小值
面积取得最小值![]() .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目



