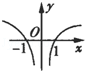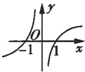题目内容
20.函数f(x)=x3-3x2+2的极大值是2.分析 先求函数的导函数,再解不等式f′(x)>0和f′(x)<0得函数的单调区间,进而由极值的定义求得函数的极值点和极值.
解答 解:∵f′(x)=3x2-3=3(x+1)(x-1),
∴函数f(x)=x3-3x在(-∞,-1)是增函数,在(-1,1)上是减函数,在(1,+∞)是增函数,
∴函数f(x)=x3-3x在x=-1时取得极大值2,
故答案为:2.
点评 利用导数工具求该函数的极值是解决该题的关键,要先确定出导函数等于零的实数x的值,再讨论出函数的单调区间,根据极值的判断方法求出该函数的极值,考查计算能力、

练习册系列答案
相关题目
10.要做一个圆锥形漏斗,其母线长为30cm,要使其体积最大,则其高应为( )
| A. | 12$\sqrt{3}$cm | B. | 10$\sqrt{3}$cm | C. | 8$\sqrt{3}$cm | D. | 5$\sqrt{3}$cm |
 在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=60°,AC=CC1=2,BC=1,E,F分别是A1C1,BC的中点.
在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=60°,AC=CC1=2,BC=1,E,F分别是A1C1,BC的中点.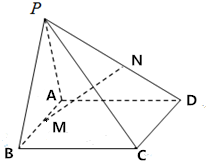 如图,四棱锥P-ABCD中,△ABC与△PAB均为等边三角形,AC=$\sqrt{2}$AD=$\sqrt{2}$CD,PC=$\frac{3}{2}$AB.
如图,四棱锥P-ABCD中,△ABC与△PAB均为等边三角形,AC=$\sqrt{2}$AD=$\sqrt{2}$CD,PC=$\frac{3}{2}$AB.