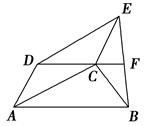
题目内容
如图, 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ 的切线,
的切线, 与
与 的延长线交于点
的延长线交于点 ,
,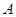 为切点.若
为切点.若 ,
,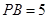 ,
, 的平分线
的平分线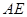 与
与 和⊙
和⊙ 分别交于点
分别交于点 、
、 ,求
,求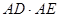 的值.
的值.
90
解析试题分析:对于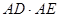 之积可以考虑两个三角形相似构造,由角平分线与等弦所对角相等即可得到三角形ACE与ABD,即
之积可以考虑两个三角形相似构造,由角平分线与等弦所对角相等即可得到三角形ACE与ABD,即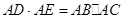 ,转化为求AC与AB长度.利用切割线定理可得AB,AC的一个等式,再利用三角形ABC为直角三角形进而得到AB,BC的另一个式子,两式即可求得相应的值,进而得到
,转化为求AC与AB长度.利用切割线定理可得AB,AC的一个等式,再利用三角形ABC为直角三角形进而得到AB,BC的另一个式子,两式即可求得相应的值,进而得到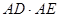 的值.再利用切割线定理与勾股定理即可得到
的值.再利用切割线定理与勾股定理即可得到 .
.
试题解析:由题得,因为AP为圆O的切线,所以由切割线定理得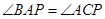 ,又
,又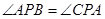 ,所以
,所以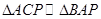 ,即
,即 ,又
,又
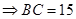 ,因为AC
,因为AC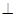 AB,所以
AB,所以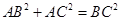
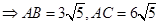 .对于三角形AEC与三角形ABD,因为
.对于三角形AEC与三角形ABD,因为 ,所以
,所以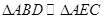 ,则
,则
 ,综上
,综上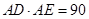 .
.
考点:相似三角形 勾股定理 切割线定理

练习册系列答案
相关题目
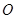 ,BD是圆
,BD是圆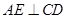 于点E,DA平分
于点E,DA平分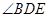 .
.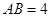 ,
,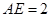 ,求CD.
,求CD.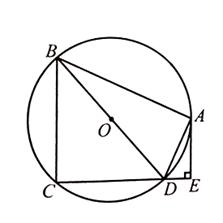

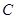 点在圆
点在圆 直径
直径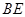 的延长线上,
的延长线上,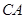 切圆
切圆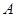 点,
点,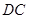 是
是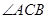 的平分线交
的平分线交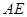 于点
于点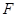 ,交
,交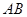 于
于 点.
点.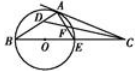
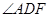 的度数;(2)若
的度数;(2)若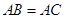 ,求
,求 .
.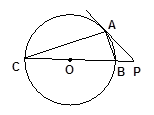
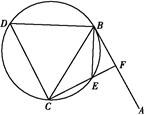
 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径. 于
于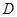 ,割线EC交圆O于B,C两点.
,割线EC交圆O于B,C两点.
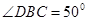 ,
,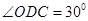 ,求
,求 的大小.
的大小.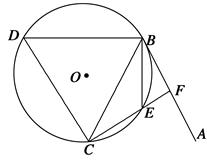
 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.