题目内容
如图,已知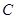 点在圆
点在圆 直径
直径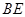 的延长线上,
的延长线上,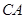 切圆
切圆 于
于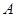 点,
点,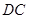 是
是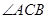 的平分线交
的平分线交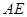 于点
于点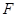 ,交
,交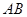 于
于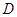 点.
点.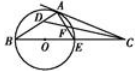
(1)求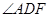 的度数;(2)若
的度数;(2)若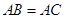 ,求
,求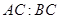 .
.
(1)45°(2)
解析试题分析:(1)由AC为圆O的切线,知∠B=∠EAC.
又DC是∠ACB的平分线,得到∠ACD=∠DCB.进一步有∠ADF=∠AFD;
由BE为圆O的直径,得∠DAE=90°,得到∠ADF=
 .
.
(2)由已知可得
 =
= ,又
,又 ,
,
得到 ,在
,在 中,
中, =
= =tan∠B=tan30°=
=tan∠B=tan30°= .
.
试题解析:(1)∵AC为圆O的切线,∴∠B=∠EAC.
又知DC是∠ACB的平分线,

即∠ADF=∠AFD,又因为BE为圆O的直径,

 . 5分
. 5分
∴ =
= ,又
,又 ,
,
∴在 中,
中, =
=

 . 10分
. 10分
考点:圆的几何性质,三角形内角平分线定理,相似三角形.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目


 是⊙
是⊙ 的直径,
的直径, 是弧
是弧 的中点,
的中点, ⊥
⊥ ,
,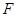 .
.
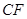 =
=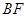 ;
;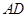 =4,⊙
=4,⊙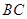 的长.
的长.
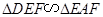 ;(2)EF//CB.
;(2)EF//CB. 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ ,
,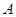 为切点.若
为切点.若 ,
,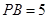 ,
, 的平分线
的平分线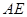 与
与 和⊙
和⊙ 、
、 ,求
,求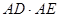 的值.
的值.

