题目内容
(12分)已知![]() .
.
(Ⅰ)当![]() 时, 求证
时, 求证![]() 在
在![]() 内是减函数;
内是减函数;
解析:(Ⅰ) ∵![]()
∴![]() ………………………1分
………………………1分
∵![]() , ∴
, ∴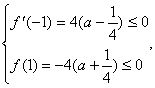 ……………………3分
……………………3分
又∵二次函数![]() 的图象开口向上,
的图象开口向上,
∴在![]() 内
内![]() , ………………………………………………………5分
, ………………………………………………………5分
故![]() 在
在![]() 内是减函数. ………………………………………………………6分
内是减函数. ………………………………………………………6分
(Ⅱ) 由(Ⅰ)知当![]() 时,
时, ![]() 在
在![]() 是减函数,故没有极值点,从而
是减函数,故没有极值点,从而![]() …8分
…8分
设![]() 在
在![]() 内的唯一极值点为
内的唯一极值点为![]() ,则
,则![]() ………………………9分
………………………9分
当![]() 时, ∵
时, ∵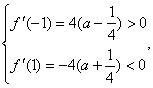
∴在![]() 内
内![]() 在
在![]() 内
内![]()
即![]() 在
在![]() 内是增函数,
内是增函数, ![]() 在
在![]() 内是减函数.
内是减函数.
当![]() 时
时![]() 在
在![]() 内有且只有一个极值点, 且是极大值点. …………10分
内有且只有一个极值点, 且是极大值点. …………10分
当![]() 时, 同理可知,
时, 同理可知, ![]() 在
在![]() 内且只有一个极值点, 且是极小值点. …11分
内且只有一个极值点, 且是极小值点. …11分

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
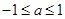 时,不等式
时,不等式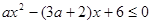 恒成立,求实数
恒成立,求实数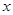 的取值范围
的取值范围 的不等式
的不等式 上的偶函数
上的偶函数 ,已知当
,已知当 时的解析式
时的解析式
 在
在 上的解析式;
上的解析式; ,
, ,且
,且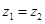 .
. 且
且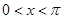
 ,求
,求 的值;
的值; =
= ,已知当
,已知当 时,
时, ,试求
,试求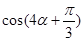 的值.
的值.