题目内容

设f(x)是定义在区间上以2为周期的函数，对,用表示区间已知当时，f(x)=x2.

（1）求f(x)在上的解析表达式;

（2）对自然数k,求集合不等的实根}

（1）（2）


解析:

解：（1）∵f(x)是以2为周期的函数，∴当时，2k也是f(x)的周期

又∵当时，，∴

即对，当时，

（2）当且时，利用（1）的结论可得方程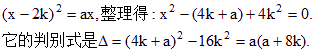

上述方程在区间上恰有两个不相等的实根的充要条件是a满足

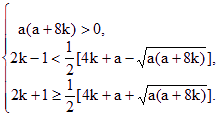
由（1）知a>0，或a<-8k.

当a>0时：因2+a>2-a，故从（2），（3）

可得即

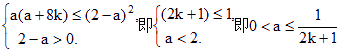
当a＜-8k时：

易知无解，

综上所述，a应满足故所求集合

练习册系列答案
相关题目
（2013•松江区一模）设f（x）是定义在R上的函数，对x∈R都有f（-x）=f（x），f（x）•f（x+2）=10，且当x∈[-2，0]时，f(x)=(
1
2
)x-1，若在区间（-2，6]内关于x的方程f（x）-loga（x+2）=0（a＞1）恰有3个不同的实数根，则a的取值范围是（　　）
（2013•天河区三模）设f（x）是定义在区间（1，+∞）上的函数，其导函数为f'（x）．如果存在实数a和函数h（x），其中h（x）对任意的x∈（1，+∞）都有h（x）＞0，使得f'（x）=h（x）（x2-ax+1），则称函数f（x）具有性质P（a）．
（1）设函数f(x)=Inx+
b+2x+1
(x＞1)，其中b为实数．
（i）求证：函数f（x）具有性质P（b）；
（ii）求函数f（x）的单调区间．
（2）已知函数g（x）具有性质P（2），给定x1，x2∈（1，+∞），x1＜x2，设m为实数，a=mx1+（1-m）x2，β=（1-m）x1+mx2，且a＞1，β＞1，若|g（a）-g（β）|＜|g（x1）-g（x2）|，求m取值范围．
（2013•顺义区二模）设定义在R上的函数f（x）是最小正周期为2π的偶函数，f′（x）是f（x）的导函数．当x∈[0，π]时，0＜f（x）＜1；当x∈（0，π）且x≠
π
2
时，(x-
π
2
)f′(x)＜0．则函数y=f（x）-cosx在[-3π，3π]上的零点个数为
6
6
．
（2013•奉贤区二模）设f（x）是定义在R上以2为周期的偶函数，已知x∈（0，1），f(x)=log
1
2
(1-x)，则函数f（x）在（1，2）上的解析式是
y=log
1
2
(x-1)
y=log
1
2
(x-1)
．

(天津六区联考模拟)设f(x)是定义在R上的单调递减的奇函数，若，，，则

[　　]

A．

B．

C．

D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网