Question

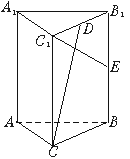
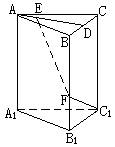
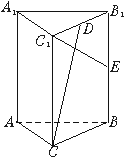
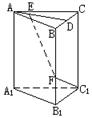
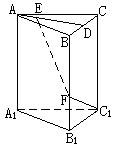
　　如图：已知直三棱柱ABC—A₁B₁C₁，AB＝AC，F为棱BB₁上一点，BF∶FB₁＝2∶1，BF＝BC＝2a。

　　（I）若D为BC的中点，E为AD上不同于A、D的任意一点，证明EF⊥FC₁；

　　（II）试问：若AB＝2a，在线段AD上的E点能否使EF与平面BB₁C₁C成60°角，为什么？证明你的结论

 

Answer 1

答案：
解析：

答案：（I）连结DF，DC1， 　　∵三棱柱ABC—A1B1C1是直三棱柱， 　　∴CC1⊥平面ABC， 　　∴平面BB1C1C⊥平面ABC 　　∵AB＝AC，D为BC的中点， 　　∴AD⊥BC，AD⊥平面BB1C1C　　∴DF为EF在平面BB1C1C上的射影， 　　在△DFC1中， 　　∵DF2＝BF2＋BD2＝5a2， 　　， 　　∴，∴DF⊥FC1 　　FC1⊥EF　　　　　　　　　　   　　　　　　　　　　　　　　　　　　　　   　　（II）∵AD⊥平面BB1C1C， 　　∴∠DFE是EF与平面BB1C1C所成的角　　　　　　　　　　　　　　　　　　 　　在△EDF中，若∠EFD＝60°， 　　则， 　　∴， 　　∴E在DA的延长线上，而不在线段AD上　　　　　　　　　　　　　　　　  　　故线段AD上的E点不能使EF与平面BB1C1C成60°角。