题目内容
设P是抛物线y=x2上的点,若P点到直线2x-y-4=0的距离最小,则P点的坐标为________.
(1,1)
[解析] 解法1:设P点坐标为(x0,x ),由点到直线的距离公式得d=
),由点到直线的距离公式得d= =
= |x
|x -2x0+4|
-2x0+4|
= |(x0-1)2+3|≥
|(x0-1)2+3|≥ .
.
由上式可知当x0=1时,dmin= .
.

∴点P的坐标为(1,1).
解法2:如图,平移2x-y-4=0这条直线至过点P与抛物线相切,则P点到直线的距离最短.
设P(x0,y0),∵y′=2x.
∴过P点的切线斜率k=y′|x=x0=2x0=2.
∴x0=1,y0=x =1,故P点坐标为(1,1).
=1,故P点坐标为(1,1).

练习册系列答案
相关题目
某中学研究性学习小组,为了考查高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了50名学生.调查结果表明:在爱看课外书的25人中有18人作文水平好,另7人作文水平一般;在不爱看课外书的25人中有6人作文水平好,另19人作文水平一般.
(1)试根据以上数据完成以下2×2列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
高中学生的作文水平与爱看课外书的2×2列联表
|
| 爱看课外书 | 不爱看课外书 | 总计 |
| 作文水平好 | |||
| 作文水平一般 | |||
| 总计 |
(2)将其中某5名爱看课外书且作文水平好的学生分别编号为1、2、3、4、5,某5名爱看课外书且作文水平一般的学生也分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
附表:
| P(K2≥k)或P(χ2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2(或χ2)=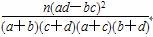
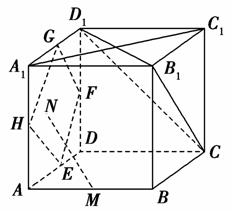
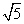 B.1:2
B.1:2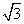 ,那么|PF|=( )
,那么|PF|=( )