题目内容
已知函数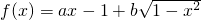 ,其中a∈{0,1},b∈{1,2},则f(x)>0在x∈[-1,0]上有解的概率为
,其中a∈{0,1},b∈{1,2},则f(x)>0在x∈[-1,0]上有解的概率为
- A.

- B.

- C.

- D.

A
分析:由题意知本题是一个等可能事件的概率,试验发生所包含的事件数是2×2=4种结果,根据所给的a,b的不同的值,列举出有解的情况,得到概率.
解答:由题意知本题是一个等可能事件的概率,
试验发生所包含的事件数是2×2=4种结果,
当a=0,b=1时,f(x)=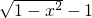 >0,即
>0,即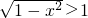 ,即1-x2>1或1-x2<-1,在x∈[-1,0]上有解,
,即1-x2>1或1-x2<-1,在x∈[-1,0]上有解,
当a=0,b=2时, >0,即
>0,即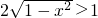 ,即
,即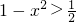 或
或 ,在x∈[-1,0]上有解,
,在x∈[-1,0]上有解,
当a=1,b=1时, >0,即
>0,即 ,在x∈[-1,0]上无解,
,在x∈[-1,0]上无解,
当a=1,b=2时,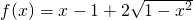 >0,即
>0,即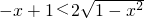 ,在x∈[-1,0]上无解,
,在x∈[-1,0]上无解,
综上可知有两个有解,
∴要求的概率是
故选A.
点评:本题看成等可能事件的概率,本题解题的关键是对于a,b的不同的值代入进行检验,判断有无解,这里的运算比较繁琐,需要认真做题.
分析:由题意知本题是一个等可能事件的概率,试验发生所包含的事件数是2×2=4种结果,根据所给的a,b的不同的值,列举出有解的情况,得到概率.
解答:由题意知本题是一个等可能事件的概率,
试验发生所包含的事件数是2×2=4种结果,
当a=0,b=1时,f(x)=
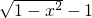 >0,即
>0,即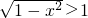 ,即1-x2>1或1-x2<-1,在x∈[-1,0]上有解,
,即1-x2>1或1-x2<-1,在x∈[-1,0]上有解,当a=0,b=2时,
 >0,即
>0,即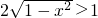 ,即
,即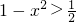 或
或 ,在x∈[-1,0]上有解,
,在x∈[-1,0]上有解,当a=1,b=1时,
 >0,即
>0,即 ,在x∈[-1,0]上无解,
,在x∈[-1,0]上无解,当a=1,b=2时,
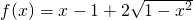 >0,即
>0,即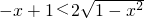 ,在x∈[-1,0]上无解,
,在x∈[-1,0]上无解,综上可知有两个有解,
∴要求的概率是

故选A.
点评:本题看成等可能事件的概率,本题解题的关键是对于a,b的不同的值代入进行检验,判断有无解,这里的运算比较繁琐,需要认真做题.

练习册系列答案
相关题目
 ,其中a>0.
,其中a>0. ,其中a是实数,设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的点,且x1<x2.
,其中a是实数,设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的点,且x1<x2.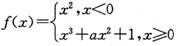 ,其中a是常数.[来源:Z|xx|k.Com]
,其中a是常数.[来源:Z|xx|k.Com]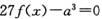 的根的
的根的