题目内容
(14分)已知函数 ,其中a是实数,设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的点,且x1<x2.
,其中a是实数,设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的点,且x1<x2.
(I)指出函数f(x)的单调区间;
(II)若函数f(x)的图象在点A,B处的切线互相垂直,且x2<0,求x2﹣x1的最小值;
(III)若函数f(x)的图象在点A,B处的切线重合,求a的取值范围.
(I)f(x)在(﹣∞,﹣1)上单调递减,在(﹣1,0)上单调递增(II)1(III)(﹣1﹣ln2,+∞)
【解析】(I)当x<0时,f(x)=(x+1)2+a,
∴f(x)在(﹣∞,﹣1)上单调递减,在(﹣1,0)上单调递增;
当x>0时,f(x)=lnx,在(0,+∞)单调递增.
(II)∵x1<x2<0,∴f(x)=x2+2x+a,∴f′(x)=2x+2,
∴函数f(x)在点A,B处的切线的斜率分别为f′(x1),f′(x2),
∵函数f(x)的图象在点A,B处的切线互相垂直,
∴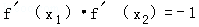 ,
,
∴(2x1+2)(2x2+2)=﹣1.
∴2x1+2<0,2x2+2>0,
∴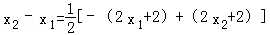
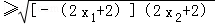 =1,当且仅当﹣(2x1+2)=2x2+2=1,即
=1,当且仅当﹣(2x1+2)=2x2+2=1,即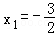 ,
,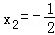 时等号成立.
时等号成立.
∴函数f(x)的图象在点A,B处的切线互相垂直,且x2<0,求x2﹣x1的最小值为1.
(III)当x1<x2<0或0<x1<x2时,∵ ,故不成立,∴x1<0<x2.
,故不成立,∴x1<0<x2.
当x1<0时,函数f(x)在点A(x1,f(x1)),处的切线方程为
 ,即
,即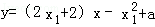 .
.
当x2>0时,函数f(x)在点B(x2,f(x2))处的切线方程为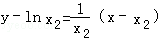 ,即
,即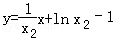 .
.
函数f(x)的图象在点A,B处的切线重合的充要条件是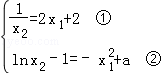 ,
,
由①及x1<0<x2可得﹣1<x1<0,
由①②得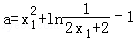 =
=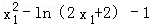 .
.
∵函数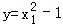 ,y=﹣ln(2x1+2)在区间(﹣1,0)上单调递减,
,y=﹣ln(2x1+2)在区间(﹣1,0)上单调递减,
∴a(x1)=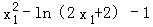 在(﹣1,0)上单调递减,且x1→﹣1时,ln(2x1+2)→﹣∞,即﹣ln(2x1+2)→+∞,也即a(x1)→+∞.
在(﹣1,0)上单调递减,且x1→﹣1时,ln(2x1+2)→﹣∞,即﹣ln(2x1+2)→+∞,也即a(x1)→+∞.
x1→0,a(x1)→﹣1﹣ln2.
∴a的取值范围是(﹣1﹣ln2,+∞).

 已知函数
已知函数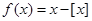 ,其中
,其中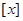 表示不超过实数
表示不超过实数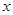 的最大整数.若关于
的最大整数.若关于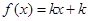 有三个不同的实根,则实数
有三个不同的实根,则实数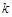 的取值范围是( )
的取值范围是( )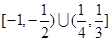 (B)
(B)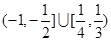
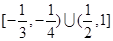 (D)
(D)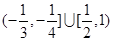
 ,
,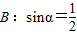 ;(2)A:x=1,B:x2+(a2-1)x-a2=0(a为实常数);(3)A:定义域为R上的函数f(x)满足f(1)>f(2),B:定义域为R的函数f(x)是单调减函数.其中A是B的充分不必要条件的是 .(填写所有满足要求的条件组的序号)
;(2)A:x=1,B:x2+(a2-1)x-a2=0(a为实常数);(3)A:定义域为R上的函数f(x)满足f(1)>f(2),B:定义域为R的函数f(x)是单调减函数.其中A是B的充分不必要条件的是 .(填写所有满足要求的条件组的序号)