题目内容
16.若满足c=2,面积S=$\frac{1}{2}$$\overrightarrow{CA}$•$\overrightarrow{CB}$的△ABC有两个,则边长BC的取值范围是(2,2$\sqrt{2}$).分析 由三角形的面积公式和向量的数量积的定义,可得C=45°,由正弦定理,令sinA<1,且a>2,即可得到所求范围.
解答 解:面积S=$\frac{1}{2}$$\overrightarrow{CA}$•$\overrightarrow{CB}$,即有
$\frac{1}{2}$absinC=$\frac{1}{2}$abcosC,
即sinC=cosC,即有tanC=1,
解得C=45°,
由正弦定理可得,$\frac{2}{sin45°}$=$\frac{a}{sinA}$,
由题意可得$\frac{\sqrt{2}}{2}$<sinC<sinA=$\frac{a}{2\sqrt{2}}$<1,即为a<2$\sqrt{2}$,
则有2<a<2$\sqrt{2}$.
故答案为:(2,2$\sqrt{2}$).
点评 本题考查三角形的面积公式和正弦定理的运用,考查向量的数量积的定义,属于中档题.

练习册系列答案
相关题目
6.正三角形ABC内一点M满足$\overrightarrow{CM}$=m$\overrightarrow{CA}$+n$\overrightarrow{CB}$,∠MCA=45°,则$\frac{m}{n}$的值为( )
| A. | $\sqrt{3}$-1 | B. | $\sqrt{3}$+1 | C. | $\frac{\sqrt{3}+1}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
5.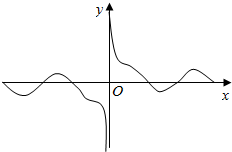 如图是函数Q(x)的图象的一部分,设函数f(x)=sinx,g(x)=$\frac{1}{x}$,则Q(x)是( )
如图是函数Q(x)的图象的一部分,设函数f(x)=sinx,g(x)=$\frac{1}{x}$,则Q(x)是( )
 如图是函数Q(x)的图象的一部分,设函数f(x)=sinx,g(x)=$\frac{1}{x}$,则Q(x)是( )
如图是函数Q(x)的图象的一部分,设函数f(x)=sinx,g(x)=$\frac{1}{x}$,则Q(x)是( )| A. | $\frac{f(x)}{g(x)}$ | B. | f (x)g (x) | C. | f (x)-g(x) | D. | f(x)+g(x) |
12.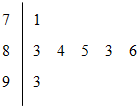 某学校2012年五四青年节举办十佳歌手赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数数与中位数分别为( )
某学校2012年五四青年节举办十佳歌手赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数数与中位数分别为( )
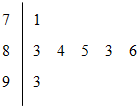 某学校2012年五四青年节举办十佳歌手赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数数与中位数分别为( )
某学校2012年五四青年节举办十佳歌手赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数数与中位数分别为( )| A. | 83,83 | B. | 83,83.5 | C. | 83,84 | D. | 84,83 |
9.设Sn为等差数列{an}的前n项和,且a1-a7+a13=6,则S13=( )
| A. | 78 | B. | 91 | C. | 39 | D. | 2015 |
10.设集合A={0,1,2,3,4},B={x∈R|$\frac{x-4}{x-2}$≤0},则A∩B=( )
| A. | {1,2,3,4} | B. | {2,3,4} | C. | {3,4} | D. | {x|2<x≤4} |