题目内容
求矩阵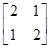
的特征值及对应的特征向量．
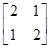的特征值及对应的特征向量．属于λ1＝1的一个特征向量为
，属于λ2＝3的一个特征向量为
.
，属于λ2＝3的一个特征向量为.特征多项式f(λ)＝
＝(λ－2)2－1＝λ2－4λ＋3
由f(λ)＝0，解得λ1＝1，λ2＝3，
将λ1＝1代入特征方程组，得
⇒x＋y＝0，
可取为属于特征值λ1＝1的一个特征向量；
同理，当λ2＝3时，由
⇒x－y＝0，
所以可取为属于特征值λ2＝3的一个特征向量．
综上所述，矩阵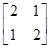有两个特征值λ1＝1，λ2＝3；
属于λ1＝1的一个特征向量为，属于λ2＝3的一个特征向量为.
＝(λ－2)2－1＝λ2－4λ＋3由f(λ)＝0，解得λ1＝1，λ2＝3，
将λ1＝1代入特征方程组，得
⇒x＋y＝0，可取
为属于特征值λ1＝1的一个特征向量；同理，当λ2＝3时，由
⇒x－y＝0，所以可取
为属于特征值λ2＝3的一个特征向量．综上所述，矩阵
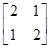有两个特征值λ1＝1，λ2＝3；属于λ1＝1的一个特征向量为
，属于λ2＝3的一个特征向量为.
练习册系列答案
相关题目
，若矩阵
所对应的变换把直线
：
变换为自身，求
．
；(2)M＝
.
+
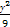=1在M-1的作用下的新曲线的方程.
,矩阵M对应的变换将点(2,1)变换成点(4,-1),求矩阵M将圆x2+y2=1变换后的曲线方程.
＝1在M－1的作用下的新曲线的方程．
，B＝
，求矩阵A－1B.
，矩阵运算
都成立，则
.
，其用途分别为
，若把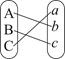
连线方式表示为
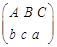，规定第一行