题目内容
19.给定两个向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$,它们的夹角为120°,|$\overrightarrow{{e}_{1}}$|=1,|$\overrightarrow{{e}_{2}}$|=2,若$\overrightarrow{a}$=2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,则|$\overrightarrow{a}$|=2.分析 根据向量模的计算和向量的数量积公式即可求出答案.
解答 解:∵$\overrightarrow{a}$=2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,|$\overrightarrow{{e}_{1}}$|=1,|$\overrightarrow{{e}_{2}}$|=2,
∴|$\overrightarrow{a}$|2=(2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)2=4$\overrightarrow{{e}_{1}}$2+$\overrightarrow{{e}_{2}}$2+4$\overrightarrow{{e}_{1}}$$\overrightarrow{{e}_{2}}$=4|$\overrightarrow{{e}_{1}}$|2+|$\overrightarrow{{e}_{2}}$|2+4|$\overrightarrow{{e}_{1}}$|•|$\overrightarrow{{e}_{2}}$|cos120°=4+4-4=4,
∴|$\overrightarrow{a}$|=2,
故答案为:2.
点评 本题考查了向量模的计算和向量的数量积的运算,属于基础题.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
9.函数y=2x+1-1的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
14.下列函数是奇函数的是( )
| A. | y=xsinx | B. | y=x2cosx | C. | y=$\frac{sinx}{x}$ | D. | y=$\frac{cosx}{x}$ |
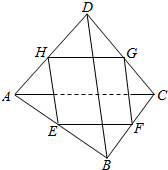 如图所示,在空间四边形ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,判断平面EG与直线BD是否平行?平面EG与直线AC是否平行?直线BD与直线AC是什么位置关系?
如图所示,在空间四边形ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,判断平面EG与直线BD是否平行?平面EG与直线AC是否平行?直线BD与直线AC是什么位置关系?