题目内容
一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示. 某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)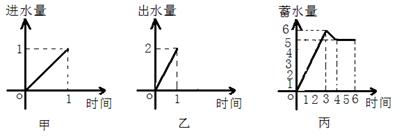
给出以下3个论断:①0点到3点只进水不出水;C②3点到4点不进水只出水;③4点到6点不进水不出水. 则正确论断的个数是( )
| A.0 | B. 1 | C. 2 | D. 3 |
B
解析试题分析:由甲,乙图得进水速度1,出水速度2,结合丙图中直线的斜率解答:只进水不出水时,蓄水量增加是2,故①对;∴不进水只出水时,蓄水量减少是2,故②不对;二个进水一个出水时,蓄水量减少也是0,故③不对;只有①满足题意,故答案为B。
考点:本题考查函数的图像和数形结合的思想。
点评:数形结合是解决此题的关键,本题容易错选成①③,其实二个进水一个出水时,蓄水量减少也是0,这是个动态中的零增量。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数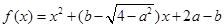 是偶函数,则函数图像与
是偶函数,则函数图像与 轴交点的纵坐标的最大值是( ).
轴交点的纵坐标的最大值是( ).
| A.- 4 | B.2 | C.3 | D.4 |
如果二次函数y=x2+mx+(m+3)有两个不同的零点,则m的取值范围是
| A.(-2,6) | B.[-2,6] |
| C.{-2,6} | D.(-∞,-2)∪(6,+∞) |
设函数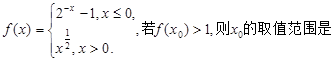 ( )
( )
| A.(-1,1) | B.(-1,+ ) ) |
C. | D. |
若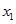 满足2x+
满足2x+ ="5,"
="5,"  满足2x+2
满足2x+2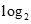 (x-1)="5,"
(x-1)="5," 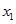 +
+ =
=
A. | B.3 | C. | D.4 |
下列函数是偶函数,且在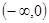 上单调递减的是( )
上单调递减的是( )
A. | B.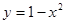 | C.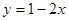 | D.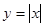 |
下列函数中,与函数 有相同定义域的是( )
有相同定义域的是( )
A. | B.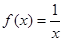  | C.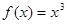 | D. |
函数f(x)= 的零点所在的区间是( )
的零点所在的区间是( )
A.(0, ) ) | B.( ,1) ,1) | C.(1, ) ) | D.( ,2) ,2) |
设函数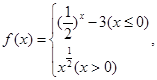 已知
已知 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |