题目内容
若DABC中，sinA:sinB:sinC = 2:3:4，那么cosC =（ ）
A． | B． | C． | D． |
A
解析试题分析：由正弦定理，令a=2k,b=3k,c=4k，
则由余弦定理得cosC=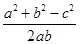
=，故选A。
考点：本题主要考查正弦定理、余弦定理。
点评：简单题，三角形中求角时，要注意角的范围。
练习册系列答案
阅读快车系列答案
相关题目
在△ABC中，若
，则
A． | B． | C． | D． |
在△ABC中，a＝3，b＝
，c＝2，那么∠B等于（ ）
| A．30° | B．45° | C．60° | D．120° |
的内角
的对边分别为
，若
,则
等于（ ）
A． | B．2 | C． | D． |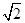
中，角
所对的边分别是
，若角依次成等差数列，且
则
等于
A． | B． | C． | D． |
在
中,若
,
,
,则
（ ）
A． | B． | C． | D． |
已知△ABC中，a＝4，b＝4
，∠A＝30°，则∠B等于（ ）
| A．30° | B．30°或150° | C．60° | D．60°或120° |
,若
，则的形状为( )
| A．等腰三角形 | B．等腰直角三角形 | C．直角三角形 | D．等边三角形 |
已知
满足
，则的形状是（ ）
| A．等腰三角形 | B．直角三角形 |
| C．等腰直角三角形 | D．等腰三角形或直角三角形 |