题目内容
在面积为2的正三角形ABC内任取一点P,则使△PBC的面积小于1的概率为分析:由题意可得,点P落在△ABC的中位线DE上及DE的下方时满足条件,而S△ADE=
×2=
,S四边形BDCE=2-
=
记“△PBC的面积小于1”为事件A,则由几何概率的计算公式可得答案.
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解答:解:作△ABC的中位线DE,点P落在直线DE上及DE的下方时满足条件
∵S△ADE=
×2=
,S四边形BDCE=2-
=
记“△PBC的面积小于1”为事件A,则P(A)=
=
=
故答案为:
∵S△ADE=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
记“△PBC的面积小于1”为事件A,则P(A)=
| SDBCE |
| S△ABC |
| ||
| 2 |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题主要考查了几何概率的计算公式在求解概率中的应用,解题的关键是要判断出复合条件的点P是在三角形的中位线及直线的下方.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
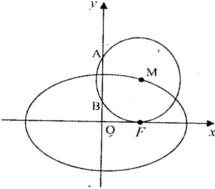 已知点F椭圆E:
已知点F椭圆E: △AOB是边长为2的正三角形,这个三角形在直线x=t左侧部分的面积为y,求函数y=f(t)的解析式.
△AOB是边长为2的正三角形,这个三角形在直线x=t左侧部分的面积为y,求函数y=f(t)的解析式.