题目内容
设直线 是曲线y=sinx(x∈(0,π))的一条切线,则实数b的值是 .
是曲线y=sinx(x∈(0,π))的一条切线,则实数b的值是 .
【答案】分析:先设切点坐标,然后对曲线进行求导,根据导数的几何意义可得到切点的坐标,代入直线方程即可求得实数b的值.
解答:解:设切点为(x,y),而y=sinx的导数为y=cosx,
在切点处的切线方程为y-y=cosx(x-x)
即y=cosx(x-x)+sinx
即得斜率为k=cosx= ,
,
∵x∈(0,π),∴x=
∴y=
代入直线方程 得b=
得b=
故答案为:
点评:本题以三角函数为载体,考查导数的几何意义,即函数在某点的导数值等于以该点为切点的切线的斜率,属基础题
解答:解:设切点为(x,y),而y=sinx的导数为y=cosx,
在切点处的切线方程为y-y=cosx(x-x)
即y=cosx(x-x)+sinx
即得斜率为k=cosx=
 ,
,∵x∈(0,π),∴x=

∴y=

代入直线方程
 得b=
得b=
故答案为:

点评:本题以三角函数为载体,考查导数的几何意义,即函数在某点的导数值等于以该点为切点的切线的斜率,属基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
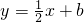 是曲线y=sinx(x∈(0,π))的一条切线,则实数b的值是________.
是曲线y=sinx(x∈(0,π))的一条切线,则实数b的值是________.